
Zadanie Maksymalne rzędy permutacji (mak)
Pomóż nam usprawnić bazę zadań!
Maksymalne rzędy permutacji
Limit pamięci: 64 MB
Permutacją  -elementową nazywamy różnowartościową funkcję
-elementową nazywamy różnowartościową funkcję
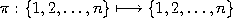 .
Rzędem permutacji
.
Rzędem permutacji  nazywamy najmniejsze takie
nazywamy najmniejsze takie 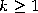 , że
dla wszystkich
, że
dla wszystkich 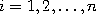 zachodzi:
zachodzi:
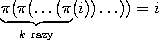
Na przykład, rzędem trzyelementowej permutacji
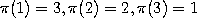 jest 2, bo
jest 2, bo 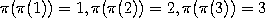 .
.
Dla zadanego  rozważmy permutacje
rozważmy permutacje  -elementowe o największym
możliwym rzędzie. Na przykład maksymalny rząd permutacji
pięcioelementowej wynosi 6. Przykładem permutacji pięcioelementowej,
której rząd wynosi 6 jest
-elementowe o największym
możliwym rzędzie. Na przykład maksymalny rząd permutacji
pięcioelementowej wynosi 6. Przykładem permutacji pięcioelementowej,
której rząd wynosi 6 jest 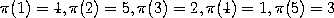 .
.
Spośród wszystkich permutacji  -elementowych o maksymalnym rzędzie chcemy
znaleźć permutację najwcześniejszą (w porządku leksykograficznym). Dokładniej,
mówimy, że permutacja
-elementowych o maksymalnym rzędzie chcemy
znaleźć permutację najwcześniejszą (w porządku leksykograficznym). Dokładniej,
mówimy, że permutacja  -elementowa
-elementowa
 jest wcześniejsza niż permutacja
jest wcześniejsza niż permutacja  -elementowa
-elementowa  ,
gdy istnieje takie
,
gdy istnieje takie 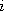 , że
, że 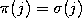 dla argumentów
dla argumentów 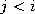 oraz
oraz 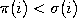 .
Najwcześniejszą permutacją pięcioelementową o rzędzie 6 jest
.
Najwcześniejszą permutacją pięcioelementową o rzędzie 6 jest
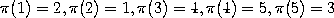 .
.
Zadanie
Napisz program, który:
-
wczyta ze standardowego wejścia zestaw liczb całkowitych
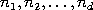 ,
,
-
dla każdej liczby
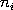 (dla
(dla 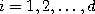 ) wyznaczy
najwcześniejszą
) wyznaczy
najwcześniejszą 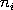 -elementową permutację o maksymalnym rzędzie,
-elementową permutację o maksymalnym rzędzie,
- wypisze na standardowe wyjście wyznaczone permutacje.
Wejście
W pierwszym wierszu standardowego wejścia znajduje się
jedna dodatnia liczba całkowita  ,
, 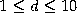 .
W kolejnych
.
W kolejnych  wierszach znajdują się dodatnie liczby całkowite
wierszach znajdują się dodatnie liczby całkowite
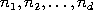 , po jednej w wierszu,
, po jednej w wierszu,
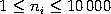 .
.
Wyjście
Twój program powinien wypisać na standardowe wyjście  wierszy.
Wiersz nr
wierszy.
Wiersz nr 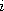 powinien zawierać ciąg liczb całkowitych oddzielonych spacjami,
będący ciągiem wartości
powinien zawierać ciąg liczb całkowitych oddzielonych spacjami,
będący ciągiem wartości 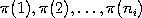 najwcześniejszej permutacji
najwcześniejszej permutacji 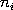 -elementowej o maksymalnym rzędzie.
-elementowej o maksymalnym rzędzie.
Przykład
Dla danych wejściowych:
2 5 14
poprawną odpowiedzią jest:
2 1 4 5 3 2 3 1 5 6 7 4 9 10 11 12 13 14 8
Autor zadania: Jakub Pawlewicz.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English