
Zadanie Obchodzenie drzewa skokami (obc)
Pomóż nam usprawnić bazę zadań!
Obchodzenie Drzewa Skokami
Limit pamięci: 32 MB
Grafem nazywamy każdą parę 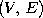 , w której
, w której 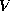 jest
skończonym zbiorem elementów zwanych wierzchołkami grafu, a
jest
skończonym zbiorem elementów zwanych wierzchołkami grafu, a 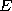 jest
podzbiorem zbioru wszystkich nieuporządkowanych par różnych wierzchołków.
Elementy zbioru
jest
podzbiorem zbioru wszystkich nieuporządkowanych par różnych wierzchołków.
Elementy zbioru 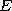 nazywamy krawędziami grafu. Jeżeli dla każdej pary
różnych wierzchołków
nazywamy krawędziami grafu. Jeżeli dla każdej pary
różnych wierzchołków  ,
,  istnieje dokładnie jeden ciąg
różnych wierzchołków
istnieje dokładnie jeden ciąg
różnych wierzchołków 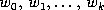 taki, że
taki, że
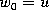 ,
, 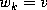 oraz pary
oraz pary 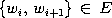 dla
dla 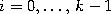 , to graf nazywamy
drzewem. O wierzchołkach
, to graf nazywamy
drzewem. O wierzchołkach  ,
,  mówi się, że są odległe w
drzewie o
mówi się, że są odległe w
drzewie o 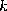 .
.
Wiadomo, że drzewo o  wierzchołkach ma dokładnie
wierzchołkach ma dokładnie 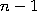 krawędzi. Drzewo
krawędzi. Drzewo 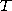 , którego wierzchołki są ponumerowane od
, którego wierzchołki są ponumerowane od
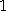 do
do  , można jednoznacznie opisać, podając liczbę
wierzchołków
, można jednoznacznie opisać, podając liczbę
wierzchołków  , a następnie odpowiedni ciąg
, a następnie odpowiedni ciąg 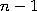 par liczb
naturalnych opisujący wszystkie jego krawędzie.
par liczb
naturalnych opisujący wszystkie jego krawędzie.
Dowolną permutację wierzchołków - to znaczy ciąg, w którym każdy wierzchołek
drzewa występuje dokładnie jeden raz - nazywamy porządkiem obchodzenia drzewa.
Jeżeli każde kolejne dwa wierzchołki w pewnym porządku są odległe w drzewie
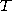 co najwyżej o
co najwyżej o  , to mówimy, że jest to porządek
obchodzenia drzewa ze skokiem
, to mówimy, że jest to porządek
obchodzenia drzewa ze skokiem  .
.
Wiadomo, że dla każdego drzewa można wyznaczyć porządek jego obchodzenia ze
skokiem 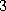 .
.
Przykład
Rysunek przedstawia drzewo o 7 wierzchołkach. Wierzchołki drzewa są reprezentowane przez czarne kropki, a krawędzie przez odcinki łączące kropki.
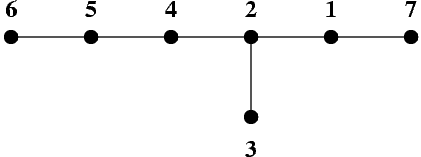
To drzewo można obejść ze skokiem 3 odwiedzając jego wierzchołki w następującym porządku: 7 2 3 5 6 4 1.
Zadanie
Ułóż program, który:
- wczytuje opis drzewa ze standardowego wejścia,
- znajduje jeden dowolny porządek obchodzenia tego drzewa ze skokiem
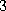 ,
, - zapisuje wyznaczony porządek na standardowym wyjściu.
Wejście
- W pierwszym wierszu standardowego wejścia jest zapisana liczba całkowita
dodatnia
 , nie większa niż
, nie większa niż 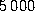 - jest to liczba
wierzchołków drzewa.
- jest to liczba
wierzchołków drzewa. - W każdym z kolejnych
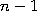 wierszy jest zapisana jedna para liczb
naturalnych oddzielonych pojedynczym odstępem, reprezentująca jedną krawędź
drzewa.
wierszy jest zapisana jedna para liczb
naturalnych oddzielonych pojedynczym odstępem, reprezentująca jedną krawędź
drzewa.
Wyjście
W kolejnych wierszach standardowego wyjścia należy zapisać numery kolejnych wierzchołków w porządku obchodzenia drzewa ze skokiem trzy - każdą liczbę należy zapisać w osobnym wierszu.
Przykład
Dla danych wejściowych:
7 1 2 2 3 2 4 4 5 5 6 1 7
poprawną odpowiedzią jest:
7 2 3 5 6 4 1
Autor zadania: Krzysztof Diks.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English