
Zadanie Inspekcja (ins)
Pomóż nam usprawnić bazę zadań!
Inspekcja
Limit pamięci: 128 MB
Sieć kolejowa Bajtockich Kolei Bitowych (BKB) składa się z dwukierunkowych odcinków torów łączących pewne pary stacji. Każda para stacji jest połączona co najwyżej jednym odcinkiem torów. Ponadto wiadomo, że z każdej stacji kolejowej można dojechać do każdej innej dokładnie jedną trasą. (Trasa może być złożona z kilku odcinków torów, ale nigdy nie przechodzi przez żadną stację więcej niż raz).
Bajtazar jest tajnym inspektorem BKB.
W celu przeprowadzenia inspekcji wybiera jedną ze stacji (oznaczmy ją 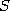 ), w której organizuje sobie centralę,
i rozpoczyna podróż po wszystkich innych stacjach.
Podróż ma następujący przebieg:
), w której organizuje sobie centralę,
i rozpoczyna podróż po wszystkich innych stacjach.
Podróż ma następujący przebieg:
-
Bajtazar zaczyna w stacji
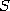 .
.
-
Następnie wybiera jedną ze stacji jeszcze nie skontrolowanych i przemieszcza się do niej po najkrótszej ścieżce,
dokonuje tam inspekcji i wraca do
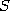 .
.
-
Nieuczciwi pracownicy BKB ostrzegają się nawzajem o przyjeździe Bajtazara.
Aby ich zmylić, następną stację do skontrolowania Bajtazar wybiera w taki sposób, aby wyjechać
w inną stronę ze stacji
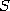 niż poprzednio, tzn. innym odcinkiem torów wychodzącym z
niż poprzednio, tzn. innym odcinkiem torów wychodzącym z 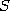 .
.
-
Każda stacja (poza stacją
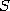 ) jest kontrolowana dokładnie raz.
) jest kontrolowana dokładnie raz.
-
Po skontrolowaniu ostatniej stacji Bajtazar nie wraca do
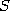 .
.
Bajtazar pragnie rozważyć wszystkie możliwe stacje jako stacje początkowe 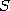 .
Dla każdej z nich chcemy wyznaczyć kolejność, w jakiej Bajtazar powinien kontrolować pozostałe stacje,
tak aby łącznie jak najmniej czasu spędził na przejazdach, o ile dla danej stacji
.
Dla każdej z nich chcemy wyznaczyć kolejność, w jakiej Bajtazar powinien kontrolować pozostałe stacje,
tak aby łącznie jak najmniej czasu spędził na przejazdach, o ile dla danej stacji 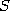 w ogóle taka kolejność istnieje.
w ogóle taka kolejność istnieje.
Wejście
Pierwszy wiersz standardowego wejścia zawiera jedną liczbę całkowitą  (
(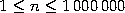 ), oznaczającą liczbę stacji.
Stacje są ponumerowane od 1 do
), oznaczającą liczbę stacji.
Stacje są ponumerowane od 1 do  .
Kolejne
.
Kolejne 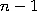 wierszy opisuje odcinki torów, po jednym w wierszu.
W każdym z nich znajdują się dwie liczby całkowite
wierszy opisuje odcinki torów, po jednym w wierszu.
W każdym z nich znajdują się dwie liczby całkowite 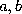 (
(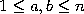 ,
, 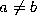 ), oddzielone pojedynczym odstępem,
oznaczające, że istnieje odcinek torów łączący stacje
), oddzielone pojedynczym odstępem,
oznaczające, że istnieje odcinek torów łączący stacje  i
i 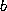 .
Każdy odcinek torów pojawia się w opisie dokładnie raz.
.
Każdy odcinek torów pojawia się w opisie dokładnie raz.
W testach wartych przynajmniej 30% punktów zachodzi dodatkowy warunek 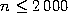 .
.
Wyjście
Twój program powinien wypisać na standardowe wyjście  wierszy, a w każdym z nich po jednej liczbie całkowitej.
Liczba w
wierszy, a w każdym z nich po jednej liczbie całkowitej.
Liczba w 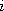 -tym wierszu powinna być równa minimalnej liczbie godzin, jakie Bajtazar musi spędzić na przejazdach,
aby skontrolować stacje, dla
-tym wierszu powinna być równa minimalnej liczbie godzin, jakie Bajtazar musi spędzić na przejazdach,
aby skontrolować stacje, dla 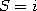 - o ile dla
- o ile dla 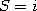 szukana kolejność stacji istnieje.
W przeciwnym przypadku, w
szukana kolejność stacji istnieje.
W przeciwnym przypadku, w 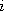 -tym wierszu powinna znaleźć się liczba
-tym wierszu powinna znaleźć się liczba 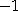 .
.
Przykład
Dla danych wejściowych:
9 3 6 2 4 2 6 2 5 1 7 2 7 8 9 7 8
poprawną odpowiedzią jest:
-1 23 -1 -1 -1 -1 -1 -1 -1
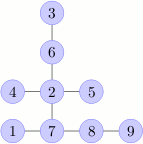
Rysunek pokazuje przykładową sieć połączeń.
Szukana kolejność, w jakiej Bajtazar powinien kontrolować stacje, istnieje tylko dla 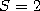 .
Może to być na przykład:
.
Może to być na przykład: 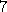 ,
,  ,
, 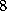 ,
, 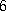 ,
, 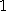 ,
, 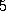 ,
, 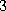 ,
, 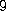 .
Przy takiej kolejności kontrolowanych stacji Bajtazar spędzi na przejazdach łącznie
.
Przy takiej kolejności kontrolowanych stacji Bajtazar spędzi na przejazdach łącznie 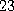 godziny.
godziny.
Autorzy zadania: Wojciech Rytter i Bartosz Szreder.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English