
Zadanie Zawody (zaw)
Pomóż nam usprawnić bazę zadań!
Zawody
Limit pamięci: 16 MB
U stóp Bajtogóry znajduje się wejście do jaskini. Jaskinia to system komnat połączonych korytarzami. Wejście do jaskini prowadzi bezpośrednio do komnaty nazywanej wejściową. Korytarze nie przecinają się (spotykają się jedynie w komnatach). Dwie komnaty mogą być albo połączone jednym korytarzem, albo mogą nie być połączone wcale (być może można jednak wtedy przejść z jednej do drugiej przechodząc po drodze przez inne komnaty). Korytarz łączy zawsze dwie różne komnaty.
Postanowiono zorganizować zawody o puchar króla Bajtocji. Celem każdego z zawodników jest przebycie dowolnie wybranej trasy w jaskini i wyjście na zewnątrz w jak najkrótszym czasie. Trasa musi przechodzić przez co najmniej jedną komnatę inną niż wejściowa. Obowiązują tylko dwie zasady: podczas wędrówki po jaskini, każdą komnatę można odwiedzić co najwyżej raz (z wyjątkiem komnaty wejściowej), podobnie tylko raz można przejść każdym z korytarzy.
Do zawodów przygotowuje się słynny grotołaz Bajtała. Bajtała długo trenował w jaskini i dokładnie poznał sieć korytarzy. Dla każdego z korytarzy wyznaczył czasy potrzebne do jego przejścia w każdą stronę. Czas potrzebny do poruszania się po komnatach można zaniedbać. Bajtała chciałby teraz wyznaczyć taką trasę spełniającą wymogi zawodów, którą można przebyć w jak najkrótszym czasie (czas potrzebny do przebycia trasy jest sumą czasów potrzebnych do przejścia korytarzy składających się na trasę).
Zadanie
Pomóż Bajtale! Napisz program, który:
- wczyta ze standardowego wejścia opis jaskini oraz czasy potrzebne do przejścia poszczególnych korytarzy,
- obliczy trasę zgodną z zasadami zawodów, dla której suma czasów przejść korytarzy składających się na trasę jest najmniejsza,
- wypisze na standardowe wyjście czas potrzebny do przejścia wyznaczonej trasy.
Wejście
W pierwszym wierszu wejścia znajdują się
dwie liczby całkowite  i
i 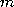 oddzielone pojedynczym odstępem,
oznaczające odpowiednio liczbę komnat w jaskini, oraz liczbę
łączących je korytarzy,
oddzielone pojedynczym odstępem,
oznaczające odpowiednio liczbę komnat w jaskini, oraz liczbę
łączących je korytarzy, 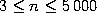 ,
, 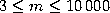 .
Komnaty są ponumerowane od
.
Komnaty są ponumerowane od 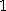 do
do  .
Komnata wejściowa ma numer
.
Komnata wejściowa ma numer 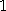 .
W kolejnych
.
W kolejnych 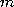 wierszach opisane są poszczególne korytarze.
W każdym z tych wierszy znajduje się czwórka liczb naturalnych
oddzielonych pojedynczymi odstępami.
Czwórka
wierszach opisane są poszczególne korytarze.
W każdym z tych wierszy znajduje się czwórka liczb naturalnych
oddzielonych pojedynczymi odstępami.
Czwórka 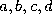 oznacza, że jaskinie
oznacza, że jaskinie  i
i 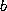 są połączone
korytarzem, czas przejścia z jaskini
są połączone
korytarzem, czas przejścia z jaskini  do
do 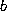 wynosi
wynosi  ,
a z
,
a z 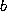 do
do  wynosi
wynosi  ,
, 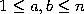 ,
, 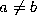 ,
,
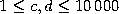 .
Możesz założyć, że zawsze istnieje przynajmniej jedna trasa spełniająca
wymogi zawodów.
.
Możesz założyć, że zawsze istnieje przynajmniej jedna trasa spełniająca
wymogi zawodów.
Wyjście
Twój program powinien wypisać w pierwszym i jedynym wierszu wyjścia jedną liczbę całkowitą - minimalny czas potrzebny do przebycia trasy spełniającej warunki zawodów.
Przykład
Dla danych wejściowych:
3 3 1 2 4 3 2 3 4 2 1 3 1 1
poprawną odpowiedzią jest:
6
Autor zadania: Łukasz Kowalik.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English