
Zadanie Jednoręki bandyta [B] (jed)
Pomóż nam usprawnić bazę zadań!
Jednoręki bandyta [B]
Limit pamięci: 128 MB
Bajtek przyszedł do kasyna, gdzie od razu zainteresował go automat do gry w jednorękiego bandytę.
Najważniejszą częścią automatu są trzy bębny.
Każdy z nich podzielony jest na  równych pól, na których namalowane są różne symbole.
Jest
równych pól, na których namalowane są różne symbole.
Jest  możliwych symboli i każdy z nich występuje na każdym bębnie dokładnie raz.
Dla uproszczenia ponumerujmy symbole liczbami od 1 do
możliwych symboli i każdy z nich występuje na każdym bębnie dokładnie raz.
Dla uproszczenia ponumerujmy symbole liczbami od 1 do  .
Poniższy rysunek przedstawia przykładowy automat z trzema bębnami podzielonymi na
.
Poniższy rysunek przedstawia przykładowy automat z trzema bębnami podzielonymi na 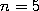 pól:
pól:
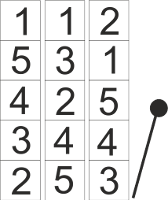
Po pociągnięciu wajchy, każdy z bębnów przesuwa się cyklicznie o pewną liczbę pozycji. Wygrana gracza zależy od liczby poziomych rzędów, w których znajdą się trzy takie same symbole.
Bajtek wie, że jednoręki bandyta może zabrać wszystkie jego pieniądze, więc wolałby najpierw stwierdzić, jaka może być jego maksymalna wygrana. Pomóż mu i wyznacz liczbę rzędów, w których mogą znaleźć się trzy takie same symbole przy najkorzystniejszym ustawieniu bębnów.
Wejście
Pierwszy wiersz wejścia zawiera jedną liczbę całkowitą  (
(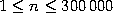 ),
oznaczającą wielkość bębnów.
Trzy następne wiersze opisują układy symboli na poszczególnych bębnach.
),
oznaczającą wielkość bębnów.
Trzy następne wiersze opisują układy symboli na poszczególnych bębnach.
Opis bębna składa się z  parami różnych liczb całkowitych
parami różnych liczb całkowitych 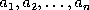 (
(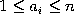 ),
gdzie
),
gdzie 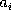 oznacza symbol znajdujący się na pozycji
oznacza symbol znajdujący się na pozycji 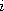 .
.
Wyjście
Pierwszy i jedyny wiersz wyjścia powinien zawierać jedną liczbę całkowitą, równą maksymalnej liczbie rzędów, w których mogą się jednocześnie znaleźć po trzy takie same symbole.
Przykład
Dla danych wejściowych:
5 1 5 4 3 2 1 3 2 4 5 2 1 5 4 3
poprawną odpowiedzią jest:
3
Wyjaśnienie do przykładu: Rysunek do testu przykładowego znajduje się w treści zadania. Bęben 1 możemy przekręcić o trzy pozycje do góry, bęben 2 o jedną pozycję do góry, a bęben 3 o jedną pozycję w dół.
Autor zadania: Jacek Tomasiewicz.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English