
Zadanie Równanie na słowach (row)
Pomóż nam usprawnić bazę zadań!
Równanie na słowach
Limit pamięci: 32 MB
Słowem dwójkowym nazywamy każdy niepusty ciąg złożony z 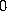 lub
lub 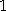 .
Równanie na słowach ma postać
.
Równanie na słowach ma postać  , gdzie
, gdzie 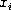 i
i 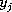 są cyframi dwójkowymi (
są cyframi dwójkowymi (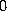 lub
lub 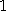 ) lub zmiennymi,
to jest małymi literami alfabetu angielskiego.
Dla każdej zmiennej jest ustalona długość słów dwójkowych, które można podstawiać w jej miejsce.
Długość tę nazywamy długością zmiennej.
Rozwiązanie równania na słowach polega na przypisaniu każdej zmiennej słowa dwójkowego o odpowiadającej tej zmiennej długości,
w taki sposób, by po zastąpieniu zmiennych w równaniu przez przypisane im słowa, obie strony równania (słowa dwójkowe) były takie same.
) lub zmiennymi,
to jest małymi literami alfabetu angielskiego.
Dla każdej zmiennej jest ustalona długość słów dwójkowych, które można podstawiać w jej miejsce.
Długość tę nazywamy długością zmiennej.
Rozwiązanie równania na słowach polega na przypisaniu każdej zmiennej słowa dwójkowego o odpowiadającej tej zmiennej długości,
w taki sposób, by po zastąpieniu zmiennych w równaniu przez przypisane im słowa, obie strony równania (słowa dwójkowe) były takie same.
Dla danego równania na słowach policz ile jest różnych rozwiązań tego równania.
Przykład
Niech 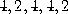 będą długościami zmiennych
będą długościami zmiennych 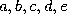 w poniższym równaniu:
w poniższym równaniu:
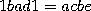 To równanie ma
To równanie ma 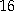 różnych rozwiązań.
różnych rozwiązań.
Zadanie
Napisz program, który:
- wczytuje ze standardowego wejścia liczbę równań i ich opisy;
- znajduję liczbę rozwiązań każdego równania;
- zapisuje wyniki na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia znajduje się liczba całkowita  ,
, 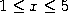 .
Jest to liczba równań.
Następne wiersze zawierają opisy
.
Jest to liczba równań.
Następne wiersze zawierają opisy  równań.
Na każdy opis składa się
równań.
Na każdy opis składa się 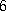 wierszy.
Między kolejnymi opisami nie ma pustych wierszy.
Każde równanie jest opisane w następujący sposób:
wierszy.
Między kolejnymi opisami nie ma pustych wierszy.
Każde równanie jest opisane w następujący sposób:
W pierwszym wierszu opisu znajduje się liczba całkowita 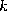 ,
, 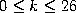 .
Jest to liczba różnych zmiennych w równaniu.
Przyjmujemy, że zawsze zmiennymi jest
.
Jest to liczba różnych zmiennych w równaniu.
Przyjmujemy, że zawsze zmiennymi jest 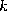 pierwszych małych liter alfabetu angielskiego.
W drugim wierszu jest zapisany ciąg
pierwszych małych liter alfabetu angielskiego.
W drugim wierszu jest zapisany ciąg 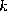 liczb całkowitych dodatnich oddzielonych pojedynczymi odstępami.
Te liczby to długości
liczb całkowitych dodatnich oddzielonych pojedynczymi odstępami.
Te liczby to długości 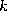 kolejnych zmiennych
kolejnych zmiennych 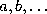 występujących w równaniu.
występujących w równaniu.
Trzeci wiersz opisu zawiera tylko jedną dodatnią liczbę całkowitą 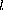 .
Jest to długość lewej strony równania — tj. długość słowa utworzonego z cyfr
.
Jest to długość lewej strony równania — tj. długość słowa utworzonego z cyfr 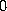 lub
lub 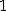 i jednoliterowych zmiennych.
W następnym wierszu jest zapisana lewa strona równania jako ciąg
i jednoliterowych zmiennych.
W następnym wierszu jest zapisana lewa strona równania jako ciąg 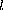 cyfr lub zmiennych bez odstępów między nimi.
Następne dwa wiersze zawierają opis prawej strony równania.
Pierwszy z tych wierszy zawiera dodatnią liczbę
cyfr lub zmiennych bez odstępów między nimi.
Następne dwa wiersze zawierają opis prawej strony równania.
Pierwszy z tych wierszy zawiera dodatnią liczbę  .
Jest to długość prawej strony równania.
Drugi z wierszy zawiera prawą stronę równania zapisaną w taki sam sposób jak jego lewa strona.
Liczba cyfr plus suma długości wszystkich zmiennych (licząc wszystkie wystąpienia każdej zmiennej) po każdej stronie równania nie przekracza
.
Jest to długość prawej strony równania.
Drugi z wierszy zawiera prawą stronę równania zapisaną w taki sam sposób jak jego lewa strona.
Liczba cyfr plus suma długości wszystkich zmiennych (licząc wszystkie wystąpienia każdej zmiennej) po każdej stronie równania nie przekracza 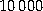 .
.
Wyjście
Dla każdego 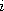 ,
, 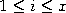 , Twój program powinien zapisać w
, Twój program powinien zapisać w 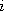 -tym wierszu standardowego wyjścia liczbę różnych rozwiązań
-tym wierszu standardowego wyjścia liczbę różnych rozwiązań 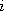 -tego równania.
-tego równania.
Przykład
Dla danych wejściowych:
1 5 4 2 4 4 2 5 1bad1 4 acbe
poprawną odpowiedzią jest:
16
Autor zadania: Wojciech Rytter.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English