
Zadanie Kangury [A] (kan)
Pomóż nam usprawnić bazę zadań!
Kangury [A]
Limit pamięci: 32 MB
Bajtazar jedzie do Australii fotografować kangury. Zaczął już przygotowania do wyjazdu i zorientował się, że może mieć problem z zabraniem całego swojego sprzętu fotograficznego. Bajtazar posiada kolekcję obiektywów o różnorodnych parametrach. Każdy obiektyw najlepiej nadaje się do fotografowania obiektów jedynie w pewnym zakresie odległości od aparatu; kangury znajdujące się w odległości spoza tego zakresu albo nie zmieszczą się w kadrze, albo będą zbyt małe.
Bajtazar zna również dokładny plan podróży: jego wyprawa przebiegać będzie przez szereg punktów obserwacyjnych. Przewodnicy Bajtazara powiedzieli mu już, jak wygląda każdy z punktów i w jakim przedziale odległości powinien się on spodziewać kangurów.
Teraz Bajtazar zastanawia się, które obiektywy zabrać ze sobą. Ponieważ bardzo nie lubi on zmieniać obiektywu w aparacie, dla każdego obiektywu chciałby obliczyć, jaki jest najdłuższy ciąg kolejnych punktów obserwacyjnych, w których ten obiektyw będzie przydatny. Obiektyw jest przydatny w danym punkcie, jeśli istnieje pewna odległość, w której można spodziewać się kangurów i która mieści się w przedziale optymalnych odległości dla tego obiektywu. Napisz program, który rozwiąże problem Bajtazara.
Wejście
W pierwszym wierszu standardowego wejścia znajdują się dwie liczby całkowite  oraz
oraz 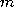 (
(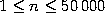 ,
,  ) oznaczające liczbę punktów obserwacyjnych oraz liczbę obiektywów w kolekcji Bajtazara.
Kolejne
) oznaczające liczbę punktów obserwacyjnych oraz liczbę obiektywów w kolekcji Bajtazara.
Kolejne  wierszy zawiera po dwie liczby całkowite
wierszy zawiera po dwie liczby całkowite 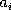 ,
, 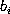 (
(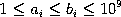 ), które oznaczają, że
w
), które oznaczają, że
w 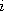 -tym punkcie obserwacyjnym kangury mogą pojawić się w odległości od
-tym punkcie obserwacyjnym kangury mogą pojawić się w odległości od 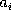 do
do 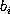 stóp bajtockich, włącznie.
stóp bajtockich, włącznie.
Dalej następuje 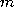 wierszy, z których każdy zawiera dwie liczby całkowite
wierszy, z których każdy zawiera dwie liczby całkowite 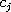 ,
, 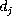 (
(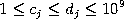 ).
Oznaczają one, że
).
Oznaczają one, że 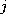 -ty obiektyw najlepiej sprawdza się przy fotografowaniu kangurów w odległości od
-ty obiektyw najlepiej sprawdza się przy fotografowaniu kangurów w odległości od 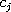 do
do 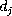 stóp bajtockich, włącznie.
stóp bajtockich, włącznie.
Wyjście
Twój program powinien wypisać na standardowe wyjście 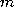 wierszy, z których
wierszy, z których 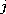 -ty powinien zawierać liczbę punktów widokowych
w najdłuższym spójnym fragmencie wyprawy, w którym Bajtazar może fotografować kangury za pomocą obiektywu numer
-ty powinien zawierać liczbę punktów widokowych
w najdłuższym spójnym fragmencie wyprawy, w którym Bajtazar może fotografować kangury za pomocą obiektywu numer 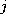 .
Obiektywy numerujemy zgodnie z kolejnością z wejścia.
.
Obiektywy numerujemy zgodnie z kolejnością z wejścia.
Przykład
Dla danych wejściowych:
3 3 2 5 1 3 6 6 3 5 1 10 7 9
poprawną odpowiedzią jest:
2 3 0
Autorzy zadania: Jakub Łącki, Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English