
Zadanie Puste prostopadłościany (pus)
Pomóż nam usprawnić bazę zadań!
Puste prostopadłościany
Limit pamięci: 32 MB
Prostopadłościan nazwiemy regularnym, gdy:
- jednym z jego wierzchołków jest punkt o współrzędnych
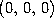 ,
, - krawędzie wychodzące z tego wierzchołka leżą na dodatnich półosiach układu współrzędnych,
- krawędzie te mają długości nie większe niż
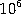 .
.
Dany jest zbiór 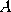 punktów przestrzeni, których wszystkie współrzędne są całkowite i należą do przedziału
punktów przestrzeni, których wszystkie współrzędne są całkowite i należą do przedziału 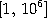 . Szukamy prostopadłościanu regularnego o maksymalnej objętości, który w swoim wnętrzu nie zawiera żadnego punktu ze zbioru
. Szukamy prostopadłościanu regularnego o maksymalnej objętości, który w swoim wnętrzu nie zawiera żadnego punktu ze zbioru 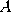 . Punkt należy do wnętrza prostopadłościanu jeżeli jest punktem prostopadłościanu, ale nie jego ściany.
. Punkt należy do wnętrza prostopadłościanu jeżeli jest punktem prostopadłościanu, ale nie jego ściany.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia współrzędne punktów ze zbioru
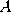 ,
, - wyznaczy jeden z prostopadłościanów regularnych o maksymalnej objętości, nie zawierający w swoim wnętrzu punktów ze zbioru
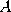 ,
, - wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia znajduje się jedna całkowita nieujemna liczba  ,
, 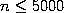 , będąca liczbą elementów zbioru
, będąca liczbą elementów zbioru 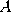 .
W kolejnych
.
W kolejnych  wierszach wejścia znajdują się trójki liczb całkowitych z przedziału
wierszach wejścia znajdują się trójki liczb całkowitych z przedziału 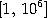 będące współrzędnymi (odpowiednio
będące współrzędnymi (odpowiednio  ,
, 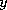 i
i  ) punktów ze zbioru
) punktów ze zbioru 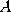 . Liczby w wierszu pooddzielane są pojedynczymi odstępami.
. Liczby w wierszu pooddzielane są pojedynczymi odstępami.
Wyjście
W jednym wierszu standardowego wyjścia powinny znaleźć się trzy liczby całkowite oddzielone pojedynczymi odstępami, będące współrzędnymi (odpowiednio  ,
, 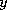 i
i  ) tego wierzchołka znalezionego prostopadłościanu regularnego, który ma wszystkie współrzędne dodatnie.
) tego wierzchołka znalezionego prostopadłościanu regularnego, który ma wszystkie współrzędne dodatnie.
Przykład
Dla danych wejściowych:
4 3 3 300000 2 200000 5 90000 3 2000 2 2 1000
poprawną odpowiedzią jest:
1000000 200000 1000
Autor zadania: Bogdan S. Chlebus.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English