
Zadanie Jedynki i zera 2 (jez)
Pomóż nam usprawnić bazę zadań!
Jedynki i zera 2
Limit pamięci: 64 MB
Pewne liczby naturalne mają zapis dziesiętny złożony tylko z jedynek i zer, w którym jest przynajmniej jedna jedynka, na przykład 101. Jeśli liczba naturalna nie ma tej własności, to można próbować pomnożyć ją przez jakąś liczbę naturalną tak, by iloczyn miał tę własność.
Zadanie
Napisz program, który dla każdej liczby naturalnej  nie większej niż
nie większej niż
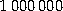 , wczytanej ze standardowego wejścia, znajduje jej
najmniejszą dodatnią wielokrotność, której zapis dziesiętny składa się
wyłącznie z zer lub jedynek, i zapisuje tę wielokrotność
w standardowym wyjściu, albo stwierdza, że takiej wielokrotności nie ma,
wpisując w standardowym wyjściu odpowiedź BRAK.
, wczytanej ze standardowego wejścia, znajduje jej
najmniejszą dodatnią wielokrotność, której zapis dziesiętny składa się
wyłącznie z zer lub jedynek, i zapisuje tę wielokrotność
w standardowym wyjściu, albo stwierdza, że takiej wielokrotności nie ma,
wpisując w standardowym wyjściu odpowiedź BRAK.
Wejście
Standardowe wejście zawiera w pierwszym wierszu całkowitą dodatnią liczbę
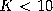 , a następnie w kolejnych wierszach ciąg
, a następnie w kolejnych wierszach ciąg 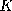 liczb
z zakresu [
liczb
z zakresu [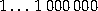 ], każda w osobnym wierszu.
], każda w osobnym wierszu.
Wyjście
Każdy kolejny wiersz standardowego wyjścia, począwszy od pierwszego, zawiera
tylko jeden wyraz BRAK albo dokładnie jedną dodatnią wielokrotność
kolejnej danej liczby w postaci ciągu cyfr 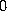 lub
lub 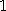 bez
odstępów pomiędzy cyframi. Rozwiązania są zapisane w standardowym wyjściu w
takiej samej kolejności jak odpowiednie liczby w standardowym wejściu.
bez
odstępów pomiędzy cyframi. Rozwiązania są zapisane w standardowym wyjściu w
takiej samej kolejności jak odpowiednie liczby w standardowym wejściu.
Przykład
Dla danych wejściowych:
6 17 11011 17 999 125 173
poprawną odpowiedzią jest:
11101 11011 11101 111111111111111111111111111 1000 1011001101
Autor zadania: Andrzej Walat.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English