
Zadanie Ewaluacja (ewa)
Pomóż nam usprawnić bazę zadań!
Ewaluacja
Limit pamięci: 128 MB
Dane jest wyrażenie matematyczne 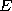 , w którym występują:
stałe od 0 do 9, zmienne od
, w którym występują:
stałe od 0 do 9, zmienne od  do
do  ,
a także operacje: dodawania, mnożenia i potęgowania o stałym wykładniku.
Co ciekawe, każda ze zmiennych
,
a także operacje: dodawania, mnożenia i potęgowania o stałym wykładniku.
Co ciekawe, każda ze zmiennych 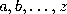 występuje w wyrażeniu
występuje w wyrażeniu
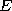 co najwyżej raz.
Zastanawiamy się, dla danej liczby pierwszej
co najwyżej raz.
Zastanawiamy się, dla danej liczby pierwszej 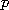 , ile pierwiastków modulo
, ile pierwiastków modulo 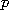 ma wielomian wyznaczony przez to wyrażenie.
Innymi słowy, pytamy, ile jest podstawień liczb od
ma wielomian wyznaczony przez to wyrażenie.
Innymi słowy, pytamy, ile jest podstawień liczb od 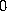 do
do 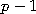 pod zmienne występujące w
pod zmienne występujące w 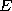 , dla których wartość wyrażenia
, dla których wartość wyrażenia 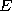 jest podzielna przez
jest podzielna przez 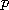 .
Ponieważ szukana liczba pierwiastków może być duża, wystarczy nam reszta z jej dzielenia
przez
.
Ponieważ szukana liczba pierwiastków może być duża, wystarczy nam reszta z jej dzielenia
przez 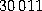 .
.
Przykładowo, wielomian reprezentowany przez wyrażenie
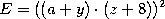
ma 15 pierwiastków modulo 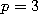 , m.in. następujące trzy pierwiastki:
, m.in. następujące trzy pierwiastki:
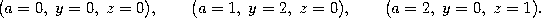
Formalnie, wyrażenie definiujemy następująco:
- Każda stała 0, 1, ..., 9 jest wyrażeniem.
- Każda zmienna a, b, ..., z jest wyrażeniem.
- Jeśli A i B są dowolnymi wyrażeniami, to wyrażeniami są także (A+B) i (A*B). Pierwsze z nich oznacza sumę wyrażeń A i B, zaś drugie - ich iloczyn.
- Jeśli A jest dowolnym wyrażeniem, a B jest stałą z zakresu 2, 3, ..., 9, to wyrażeniem jest także (A^B) (wyrażenie A do potęgi B).
Wejście
Pierwszy wiersz wejścia zawiera jedną liczbę pierwszą 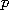 (
(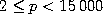 ).
Drugi wiersz zawiera wyrażenie
).
Drugi wiersz zawiera wyrażenie 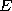 zgodne z podaną specyfikacją, opisane przez
ciąg złożony z co najwyżej 300 znaków
0, 1, ..., 9, a, b, ..., z,
+, *, ^,
(, ).
W podanym ciągu nie występują odstępy.
zgodne z podaną specyfikacją, opisane przez
ciąg złożony z co najwyżej 300 znaków
0, 1, ..., 9, a, b, ..., z,
+, *, ^,
(, ).
W podanym ciągu nie występują odstępy.
Wyjście
Oznaczmy przez 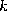 liczbę pierwiastków modulo
liczbę pierwiastków modulo 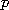 wielomianu
wielomianu 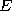 .
Twój program powinien wypisać jedną nieujemną liczbę całkowitą: resztę z dzielenia
.
Twój program powinien wypisać jedną nieujemną liczbę całkowitą: resztę z dzielenia 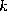 przez
przez 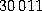 .
.
Przykład
Dla danych wejściowych:
3 (((a+y)*(z+8))^2)
poprawną odpowiedzią jest:
15
Autor zadania: Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English