Straight Lines 2

Memory limit: 64 MB

By the distance from a given straight line to a polygon we mean the smallest distance of any point of the polygon from this straight line (by the polygon we understand both its edges and its interior). The polygon does not need to be convex, it can also have multiple vertices and self-crossings of its boundary.

Task

Write a program which:

• reads from the standard input the description of the polygon and description of some number of straight lines,
• for each straight line calculates the distance from that line to the polygon,
• writes result to the standard output.

Output

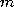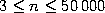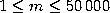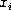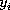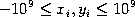In the first line of the standard input there are two integers and (, ), separated by a single space and representing the number of sides of the polygon and the number of straight lines to be analyzed. Each of the following lines contains two integers and (), separated by a single space and representing coordinates of the 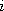'th vertex of the polygon. Pairs of consecutive vertices, as well as the first and the last vertex, define sides of the polygon. Each of the following 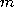lines contains three integers 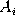, 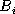and 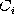(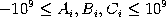, 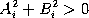), separated by single spaces and representing a straight line defined by equation .

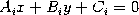Output

Your program should print 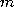lines to the standard output. 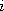'th line should contain the square of the distance between -th straight line and the polygon, written as an irreducible fraction, where numerator is separated from denominator by the sign.

Example

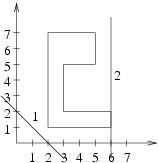
For the input data:

8 2
2 1
6 1
6 2
3 2
3 5
5 5
5 7
2 7
1 1 -2
1 0 -6

the correct result is:

1/2
0/1

Task author: Jakub Radoszewski.