
Zadanie Dekompozycja acykliczna (dek)
Pomóż nam usprawnić bazę zadań!
Acyclic Decomposition
Memory limit: 32 MB
Byteman is studying directed graphs. He especially likes graphs which do not contain cycles, since this is a class of graphs in which many problems can be solved easily and effectively. Now he is trying to find a method of representing any directed graph as a sum of acyclic graphs.
For a given directed graph he is trying to find a way to divide the set of its edges into a minimal number of subsets in such a way that the graphs constructed using the respective subsets of edges do not contain cycles. Could you write a program which solves Byteman's problem?
Input
The first line of the standard input contains two integers  and
and 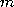 (
(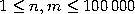 ), denoting the number of vertices and the number of edges in the graph, respectively.
The vertices are numbered from
), denoting the number of vertices and the number of edges in the graph, respectively.
The vertices are numbered from  to
to  .
Each of the following
.
Each of the following  lines contains a description of one edge of the graph as a pair of integers
lines contains a description of one edge of the graph as a pair of integers
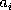 ,
, 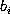 (
(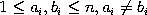 ).
Such a pair denotes a directed edge of the graph from the vertex
).
Such a pair denotes a directed edge of the graph from the vertex 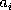 to the vertex
to the vertex 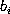 .
You may assume that the graph does not contain multiple edges.
.
You may assume that the graph does not contain multiple edges.
Output
The first line of the standard output should contain a single integer 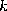 -
the minimal number of acyclic graphs in any decomposition of the graph.
% BGOR : wprowadzona poprawka na prośbę JRAD
Each of the following
-
the minimal number of acyclic graphs in any decomposition of the graph.
% BGOR : wprowadzona poprawka na prośbę JRAD
Each of the following 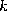 lines should contain a description of one element of the decomposition,
starting with an integer
lines should contain a description of one element of the decomposition,
starting with an integer 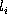 denoting the number of edges in the
denoting the number of edges in the 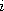 th element.
It should be followed by an increasing sequence of
th element.
It should be followed by an increasing sequence of 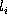 numbers of edges belonging to the
numbers of edges belonging to the
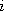 th element of the decomposition.
The edges are numbered from
th element of the decomposition.
The edges are numbered from 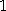 to
to 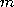 in the order in which they appear in the input.
Each edge should be present in exactly one element of the decomposition.
in the order in which they appear in the input.
Each edge should be present in exactly one element of the decomposition.
If there are multiple correct solutions, your program should output any one of them.
Example
For the input data:
6 5 1 2 2 3 3 1 4 5 5 4
the correct result is:
2 2 3 5 3 1 2 4
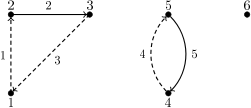
Illustration of the example from the task statement.
The circles represent the vertices, while the lines and arcs (continuous and dashed) represent
the edges of the graph.
The numbers next to the circles are the numbers of the vertices, and the numbers next to
the lines/arcs are the numbers of edges.
This graph can be decomposed into two acyclic graphs: the edges of the first one are
denoted by continuous lines/arcs and the edges of the second one - by dashed lines/arcs.
Task author: Jakub Lacki.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English