
Zadanie Zamek (zam)
Pomóż nam usprawnić bazę zadań!
Zamek
Limit pamięci: 32 MB
Poszukiwacze skarbów zdobyli mapę zamku, w którego podziemiach znajduje się olbrzymi skarb.
Mapa jest naniesiona na siatkę kwadratową, której węzły mają współrzędne całkowite.
Lewy dolny róg (węzeł) siatki ma współrzędne 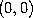 , a przeciwległy, prawy górny róg — współrzędne
, a przeciwległy, prawy górny róg — współrzędne 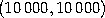 .
Na mapie zamek ma kształt wielokąta, którego boki leżą na liniach siatki.
Kolejne dwa boki wielokąta są zawsze prostopadłe.
Brzeg tego wielokąta jest łamaną zamkniętą zwykłą, tzn. każdy jej wierzchołek należy do dokładnie dwóch odcinków łamanej,
a każdy inny punkt — do jednego.
Odcinki linii tworzących siatkę zawarte w wielokącie, w tym także każdy bok wielokąta, przedstawiają odcinki podziemnych korytarzy zamku.
W jednym z węzłów (tzn. na przecięciu linii siatki), należącym do wielokąta zaznaczony jest punkt wejścia do podziemi,
a w innym węźle również należącym do wielokąta — punkt, w którym ukryty jest skarb.
.
Na mapie zamek ma kształt wielokąta, którego boki leżą na liniach siatki.
Kolejne dwa boki wielokąta są zawsze prostopadłe.
Brzeg tego wielokąta jest łamaną zamkniętą zwykłą, tzn. każdy jej wierzchołek należy do dokładnie dwóch odcinków łamanej,
a każdy inny punkt — do jednego.
Odcinki linii tworzących siatkę zawarte w wielokącie, w tym także każdy bok wielokąta, przedstawiają odcinki podziemnych korytarzy zamku.
W jednym z węzłów (tzn. na przecięciu linii siatki), należącym do wielokąta zaznaczony jest punkt wejścia do podziemi,
a w innym węźle również należącym do wielokąta — punkt, w którym ukryty jest skarb.
Chcemy obliczyć długość najkrótszej drogi podziemnymi korytarzami zamku od punktu wejścia do podziemi do punktu, w którym ukryty jest skarb. Przyjmujemy, że jednostką długości jest długość boku pojedynczej kratki na siatce.
Zadanie
Napisz program, który:
- wczytuje ze standardowego wejścia następujące dane o zamku:
- liczbę wierzchołków
 wielokąta przedstawiającego zamek,
wielokąta przedstawiającego zamek, 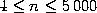 ,
,
- współrzędne wierzchołków w kolejności ich występowania przy obchodzeniu wielokąta,
- współrzędne punktu wejścia do podziemi i punktu, w którym ukryty jest skarb;
- liczbę wierzchołków
- znajduje długość najkrótszej drogi podziemnymi korytarzami zamku (po liniach siatki), od punktu wejścia do podziemi do punktu, w którym znajduje się skarb;
- zapisuje wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia jest zapisana jedna liczba całkowita  z zakresu
z zakresu 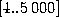 —
jest to liczba wierzchołków wielokąta przedstawiającego zamek.
W każdym z kolejnych
—
jest to liczba wierzchołków wielokąta przedstawiającego zamek.
W każdym z kolejnych  wierszy są zapisane dwie liczby całkowite z zakresu
wierszy są zapisane dwie liczby całkowite z zakresu 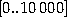 oddzielone pojedynczym odstępem
— są to współrzędne kolejnego wierzchołka wielokąta.
oddzielone pojedynczym odstępem
— są to współrzędne kolejnego wierzchołka wielokąta.
Następnie, w przedostatnim wierszu pliku są zapisane w takim samym formacie współrzędne punktu wejścia do podziemi, a w ostatnim wierszu współrzędne punktu położenia skarbu.
Wyjście
W pierwszym i jedynym wierszu standardowego wyjścia należy zapisać jedną liczbę całkowitą — długość najkrótszej drogi od punktu wejścia do podziemi do punktu w którym ukryty jest skarb.
Przykład
Dla danych wejściowych:
10 9 6 9 2 12 2 12 9 2 9 2 1 8 1 8 3 4 3 4 6 11 5 3 1
poprawną odpowiedzią jest:
14
Autor zadania: Krzysztof Diks.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English