
Zadanie PIN (pin)
Pomóż nam usprawnić bazę zadań!
PIN
Limit pamięci: 256 MB
Marcin został administratorem sieci w dużej firmie. Firma ta nie zmieniała systemu autoryzacji pracowników od lat 80. XX wieku. Każdy pracownik ma przypisany czterocyfrowy numer PIN. Nie funkcjonują natomiast żadne nazwy użytkowników ani hasła, jedynym sposobem logowania jest wpisanie swojego PIN-u. Wraz z rozwojem firmy dodano możliwość używania liter, ale PIN nadal składa się tylko z czterech znaków.
Marcin jest niezadowolony z istniejącej sytuacji. Załóżmy bowiem, że w firmie jest dwoje pracowników, których PIN-y różnią się tylko na jednej pozycji, np. 61ab oraz 62ab. Jeśli pierwszy z nich przypadkowo wciśnie 2 zamiast 1, system zaloguje go jako tego drugiego pracownika. Marcin chciałby poznać statystyki dotyczące aktualnie używanych w firmie PIN-ów, w szczególności obliczyć, ile jest par PIN-ów, które różnią się odpowiednio na 1, 2, 3 albo 4 pozycjach. Ma nadzieję, że te statystyki będą na tyle alarmujące, że uda się przekonać szefa do wymiany systemu autoryzacji na lepszy.
Zadanie
Masz daną listę PIN-ów oraz liczbę całkowitą 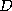 .
Znajdź liczbę par PIN-ów, które różnią się na dokładnie
.
Znajdź liczbę par PIN-ów, które różnią się na dokładnie 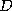 pozycjach.
pozycjach.
Specyfikacja wejścia
Pierwszy wiersz wejścia zawiera dwie liczby całkowite dodatnie 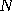 oraz
oraz
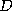 oddzielone pojedynczym odstępem, przy czym
oddzielone pojedynczym odstępem, przy czym 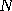 jest liczbą PIN-ów, a
jest liczbą PIN-ów, a 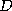 jest wybraną
liczbą różniących się pozycji w PIN-ach.
Każdy z kolejnych
jest wybraną
liczbą różniących się pozycji w PIN-ach.
Każdy z kolejnych 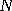 wierszy zawiera jeden PIN.
wierszy zawiera jeden PIN.
Ograniczenia
Możesz założyć, że we wszystkich testach zachodzi 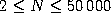 oraz
oraz 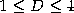 .
.
Każdy PIN ma długość 4, a każdy jego znak jest albo cyfrą, albo małą literą od 'a' do 'z' włącznie. Możesz założyć, że wszystkie PIN-y na wejściu są różne.
W testach wartych 15 punktów zachodzi 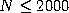 .
.
W testach wartych 60 punktów zachodzi  .
Wśród nich znajdują się testy warte 30 punktów, w których
.
Wśród nich znajdują się testy warte 30 punktów, w których 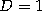 .
.
W testach wartych 75 punktów każdy PIN składa się jedynie z cyfr lub małych liter 'a' do 'f' włącznie. Może więc być traktowany jako liczba w zapisie szesnastkowym.
Specyfikacja wyjścia
Wypisz pojedynczy wiersz zawierający jedną liczbę oznaczającą liczbę par PIN-ów, które różnią się na
dokładnie 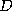 pozycjach.
pozycjach.
Przykłady
Dla danych wejściowych:
4 1 0000 a010 0202 a0e2
poprawną odpowiedzią jest:
0
Każda para spośród tych PIN-ów różni się na więcej niż jednej pozycji.
Dla danych wejściowych:
4 2 0000 a010 0202 a0e2
poprawną odpowiedzią jest:
3
Są trzy pary PIN-ów różniące się na dokładnie dwóch pozycjach: (0000, a010), (0000, 0202) i (a010, a0e2).
Autor zadania: Lukas Polacek.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English