Empty Cuboids

Memory limit: 32 MB

We call a cuboid regular if:

• one of its vertices is a point with coordinates ,
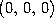• edges beginning in this vertex lay on positive semi-axes of the coordinate system,
• the edges are not longer than .

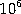There is given a set 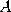of points of space, which coordinates are integers from the interval 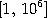. We try to find a regular cuboid of maximal volume, which does not contain any of the points from the set 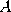. A point belongs to the cuboid if it belongs to the inside of the cuboid, i.e. it is a point of the cuboid, but not of its wall.

Task

Write a program which:

• reads from the standard input coordinates of points from the set ,
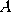• finds one of the regular cuboids of maximal volume, which does not contain any points from the set ,
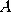• writes the result to the standard output.

Input

In the first line of the standard input one non-negative integer , , 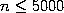is written. It is the number of elements in the set 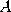. In the following lines of the input there are triples of integers from the interval 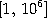, which are coordinates (respectively , 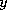and ) of points from . Numbers in each line are separated by single spaces.

Output

In the only line of the standard output there should be three integers separated by single spaces. These are coordinates (respectively , 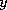and ) of the vertex of the regular cuboid of maximal volume. We require that coordinates are positive.

Example

For the input data:

4
3 3 300000
2 200000 5
90000 3 2000
2 2 1000

the correct result is:

1000000 200000 1000

Task author: Bogdan S. Chlebus.