
Zadanie Parking (gar)
Pomóż nam usprawnić bazę zadań!
Parking
Limit pamięci: 32 MB
Na pewnym parkingu znajduje się 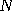 miejsc ponumerowanych od
miejsc ponumerowanych od 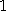 do
do 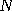 .
Mechanizm działania tego parkingu jest następujący.
Każdego ranka przed otwarciem parking jest pusty.
Jak tylko jakiś samochód przyjeżdża na parking, stróże sprawdzają, czy są
jakieś wolne miejsca parkingowe.
Jeżeli nie, to samochód musi czekać przy wjeździe na zwolnienie się jakiegoś miejsca.
Jeśli jakieś miejsce parkingowe jest wolne lub w momencie, gdy któreś staje
się wolne, samochód zostaje zaparkowany na wolnym miejscu.
Jeżeli istnieje więcej niż jedno wolne miejsce parkingowe, samochód parkuje
w miejscu o najmniejszym numerze.
Jeśli jakiś samochód oczekuje na miejsce i w tym czasie przybywa więcej
samochodów, wszystkie one ustawiają się w kolejce przy wjeździe w kolejności,
w której przyjechały.
Jeśli wówczas jakieś miejsce parkingowe zwolni się, parkuje tam pierwszy
w kolejce samochód (tzn. ten, który przybył najwcześniej).
.
Mechanizm działania tego parkingu jest następujący.
Każdego ranka przed otwarciem parking jest pusty.
Jak tylko jakiś samochód przyjeżdża na parking, stróże sprawdzają, czy są
jakieś wolne miejsca parkingowe.
Jeżeli nie, to samochód musi czekać przy wjeździe na zwolnienie się jakiegoś miejsca.
Jeśli jakieś miejsce parkingowe jest wolne lub w momencie, gdy któreś staje
się wolne, samochód zostaje zaparkowany na wolnym miejscu.
Jeżeli istnieje więcej niż jedno wolne miejsce parkingowe, samochód parkuje
w miejscu o najmniejszym numerze.
Jeśli jakiś samochód oczekuje na miejsce i w tym czasie przybywa więcej
samochodów, wszystkie one ustawiają się w kolejce przy wjeździe w kolejności,
w której przyjechały.
Jeśli wówczas jakieś miejsce parkingowe zwolni się, parkuje tam pierwszy
w kolejce samochód (tzn. ten, który przybył najwcześniej).
Koszt zaparkowania samochodu (w dolarach) jest iloczynem jego masy wyrażonej w kilogramach oraz stawki związanej z jego miejscem parkingowym. Koszt ten nie zależy od tego, jak długo samochód pozostaje na parkingu.
Właściciel parkingu wie, że dzisiaj przybędzie tam 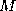 samochodów, a także
zna kolejność ich przyjazdów i wyjazdów.
Pomóż mu obliczyć, na ile dolarów zysku może dzisiaj liczyć.
samochodów, a także
zna kolejność ich przyjazdów i wyjazdów.
Pomóż mu obliczyć, na ile dolarów zysku może dzisiaj liczyć.
Zadanie
Napisz program, który mając dane stawki związane z miejscami parkingowymi, masy samochodów oraz kolejność, w której samochody przyjeżdżają i wyjeżdżają, obliczy łączny zysk właściciela parkingu.
Ograniczenia
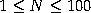 - liczba miejsc parkingowych
- liczba miejsc parkingowych
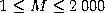 - liczba samochodów
- liczba samochodów
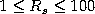 - stawka za miejsce parkingowe
- stawka za miejsce parkingowe  , w dolarach na kilogram
, w dolarach na kilogram
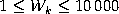 - masa samochodu
- masa samochodu  , w kilogramach
, w kilogramach
Wejście
Twój program powinien wczytać ze standardowego wejścia następujące dane:
- Pierwszy wiersz zawiera liczby całkowite
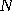 oraz
oraz 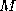 oddzielone
pojedynczym odstępem.
oddzielone
pojedynczym odstępem.
- Kolejne
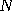 wierszy opisuje stawki za poszczególne miejsca parkingowe.
wierszy opisuje stawki za poszczególne miejsca parkingowe.
 -ty z tych wierszy zawiera jedną liczbę całkowitą
-ty z tych wierszy zawiera jedną liczbę całkowitą 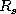 - stawkę
za miejsce parkingowe numer
- stawkę
za miejsce parkingowe numer  , w dolarach na kilogram.
, w dolarach na kilogram.
- Kolejne
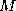 wierszy opisuje masy samochodów.
Samochody są ponumerowane od
wierszy opisuje masy samochodów.
Samochody są ponumerowane od 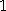 do
do 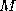 w jakiejkolwiek kolejności.
w jakiejkolwiek kolejności.
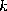 -ty z tych
-ty z tych 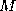 wierszy zawiera jedną liczbę całkowitą
wierszy zawiera jedną liczbę całkowitą 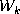 -
masę samochodu numer
-
masę samochodu numer 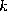 , w kilogramach.
, w kilogramach.
- Kolejne
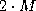 wierszy opisuje przyjazdy i wyjazdy wszystkich
samochodów w porządku chronologicznym.
Dodatnia liczba całkowita
wierszy opisuje przyjazdy i wyjazdy wszystkich
samochodów w porządku chronologicznym.
Dodatnia liczba całkowita 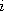 oznacza, że samochód numer
oznacza, że samochód numer 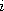 przyjeżdża na parking.
Ujemna liczba całkowita
przyjeżdża na parking.
Ujemna liczba całkowita 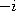 oznacza, że samochód numer
oznacza, że samochód numer 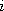 wyjeżdża z parkingu.
Żaden samochód nie wyjedzie z parkingu przed swoim przyjazdem i każdy
z
wyjeżdża z parkingu.
Żaden samochód nie wyjedzie z parkingu przed swoim przyjazdem i każdy
z 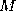 samochodów pojawi się dokładnie dwukrotnie w tym ciągu,
z czego pierwsze pojawienie będzie oznaczało przyjazd, a drugie wyjazd.
Dodatkowo, żaden samochód nie wyjedzie z parkingu przed zaparkowaniem
(tzn. nigdy nie wyjedzie żaden samochód oczekujący w kolejce).
samochodów pojawi się dokładnie dwukrotnie w tym ciągu,
z czego pierwsze pojawienie będzie oznaczało przyjazd, a drugie wyjazd.
Dodatkowo, żaden samochód nie wyjedzie z parkingu przed zaparkowaniem
(tzn. nigdy nie wyjedzie żaden samochód oczekujący w kolejce).
Wyjście
Twój program powinien wypisać na standardowe wyjście jeden wiersz zawierający jedną liczbę całkowitą: łączną liczbę dolarów, które zarobi dziś właściciel parkingu.
Ocenianie
W testach wartych 40 punktów, w momencie przyjazdu każdego samochodu będzie co najmniej jedno wolne miejsce parkingowe. W tych testach żaden samochód nie będzie musiał czekać na miejsce.
Przykład
Dla danych wejściowych:
3 4 2 3 5 200 100 300 800 3 2 -3 1 4 -4 -2 -1
poprawną odpowiedzią jest:
5300
Wyjaśnienie do przykładu: Samochód numer 3 zajmuje miejsce numer 1 i płaci 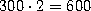 dolarów.
dolarów.
Samochód numer 2 zajmuje miejsce numer 2 i płaci 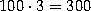 dolarów.
dolarów.
Samochód numer 1 zajmuje miejsce numer 1
(które zostało zwolnione przez samochód numer 3) i płaci 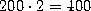 dolarów.
dolarów.
Samochód numer 4 zajmuje miejsce numer 3 (ostatnie wolne)
i płaci 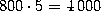 dolarów.
dolarów.
Dla danych wejściowych:
2 4 5 2 100 500 1000 2000 3 1 2 4 -1 -3 -2 -4
poprawną odpowiedzią jest:
16200
Wyjaśnienie do przykładu: Samochód numer 3 zajmuje miejsce numer 1 i płaci 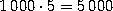 dolarów.
dolarów.
Samochód numer 1 zajmuje miejsce numer 2 i płaci 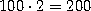 dolarów.
dolarów.
Samochód numer 2 przyjeżdża i musi poczekać przy wjeździe.
Samochód numer 4 przyjeżdża i musi poczekać przy wjeździe za samochodem numer 2.
Kiedy samochód numer 1 zwalnia swoje miejsce parkingowe, samochód numer 2
zajmuje je i płaci 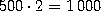 dolarów.
dolarów.
Kiedy samochód numer 3 zwalnia swoje miejsce parkingowe, samochód numer 4
zajmuje je i płaci 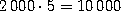 dolarów.
dolarów.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English