
Zadanie Automorfizmy [B] (aut)
Pomóż nam usprawnić bazę zadań!
Automorphisms [B]
Memory limit: 128 MB
A tree is an undirected graph in which any two nodes are connected with at most one simple path, that is, a path without repeating nodes.
Consider a tree with  nodes numbered
nodes numbered 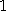 through
through  .
Let
.
Let 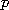 be a permutation of the set of nodes of the tree, that is,
a one-to-one function (injection)
be a permutation of the set of nodes of the tree, that is,
a one-to-one function (injection)
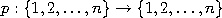 .
The permutation
.
The permutation 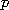 is called an automorphism if for any two nodes
is called an automorphism if for any two nodes  ,
,  of the tree, the nodes
of the tree, the nodes 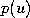 and
and 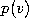 are connected with an edge
if and only if
are connected with an edge
if and only if  and
and  are connected with an edge.
are connected with an edge.
We would like to know what is the number of different automorphisms of
a given tree modulo 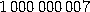 .
.
Input
The first line of the standard input contains an integer  (
(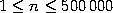 ): the number of nodes of the tree.
Each of the following
): the number of nodes of the tree.
Each of the following 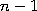 lines contains two integers
lines contains two integers 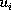 and
and 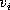 (
(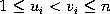 ) that represent an edge connecting the nodes
) that represent an edge connecting the nodes
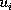 and
and 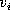 .
.
Output
The first and only line of the standard output should contain one integer: the
number of different automorphisms of the given tree modulo 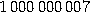 .
.
Example
For the input data:
6 1 3 2 3 3 4 4 5 4 6
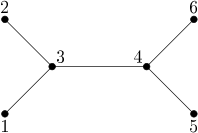
the correct result is:
8
Explanation of the example: This tree has 8 automorphisms, in particular, the following three:
-
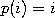 for
for 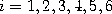
-
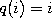 for
for 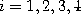 ,
, 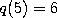 ,
, 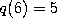
-
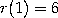 ,
, 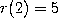 ,
, 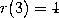 ,
, 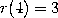 ,
, 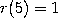 ,
, 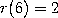 .
.
Task author: Adam Malinowski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English