
Zadanie Ciągi bez zająknięć (cia)
Pomóż nam usprawnić bazę zadań!
Ciągi bez zająknięć
Limit pamięci: 32 MB
Rozważamy ciągi liter.
Powiemy, że ciąg 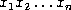 zawiera zająknięcie,
jeśli napotykamy w nim dwa, następujące bezpośrednio po sobie,
wystąpienia takiego samego podciągu.
Tzn. jeśli dla pewnych
zawiera zająknięcie,
jeśli napotykamy w nim dwa, następujące bezpośrednio po sobie,
wystąpienia takiego samego podciągu.
Tzn. jeśli dla pewnych 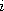 i
i 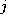 (
(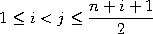 )
zachodzi:
)
zachodzi: 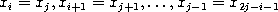 .
.
Interesują nas  -elementowe ciągi bez zająknięć
o minimalnej liczbie liter.
-elementowe ciągi bez zająknięć
o minimalnej liczbie liter.
Przykład
Dla 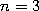 wystarczą dwie litery, powiedzmy
wystarczą dwie litery, powiedzmy  i
i 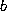 .
Mamy dokładnie dwa 3-elementowe ciągi bez zająknięć złożone
z takich liter:
.
Mamy dokładnie dwa 3-elementowe ciągi bez zająknięć złożone
z takich liter: 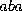 i
i 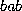 .
Dla
.
Dla 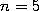 potrzebne są już 3 różne litery.
Na przykład
potrzebne są już 3 różne litery.
Na przykład 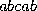 jest trójliterowym ciągiem bez zająknięć.
W ciągu
jest trójliterowym ciągiem bez zająknięć.
W ciągu 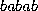 mamy dwa zająknięcia:
mamy dwa zająknięcia: 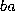 i
i 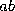 .
.
Zadanie
Napisz program, który:
-
wczyta długość ciągu
 ,
,
-
obliczy
 -elementowy ciąg bez zająknięć o minimalnej
liczbie różnych liter,
-elementowy ciąg bez zająknięć o minimalnej
liczbie różnych liter,
- wypisze wynik.
Wejście
W pierwszym wierszu standardowego wejścia zapisana jest
jedna dodatnia liczba całkowita  ,
, 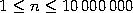 .
.
Wyjście
Twój program powinien pisać na standardowe wyjście.
W pierwszym wierszu powinna zostać wypisana
jedna dodatnia liczba całkowita 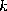 ,
równa minimalnej liczbie różnych liter, które muszą wystąpić
w
,
równa minimalnej liczbie różnych liter, które muszą wystąpić
w  -elementowym ciągu nie zawierającym zająknięć.
-elementowym ciągu nie zawierającym zająknięć.
W drugim wierszu należy wypisać obliczony ciąg bez zająknięć, jako
słowo złożone z  małych liter alfabetu angielskiego,
od litery
małych liter alfabetu angielskiego,
od litery  do
do 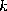 -tej litery alfabetu.
Jeżeli istnieje wiele takich ciągów, Twój program powinien wypisać
jeden z nich.
-tej litery alfabetu.
Jeżeli istnieje wiele takich ciągów, Twój program powinien wypisać
jeden z nich.
Możesz przyjąć, że 26 liter wystarczy.
Przykład
Dla danych wejściowych:
5
poprawną odpowiedzią jest:
3 abcab
Autor zadania: Krzysztof Sikora.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English