
Zadanie Nawiasy (naw)
Pomóż nam usprawnić bazę zadań!
Brackets
Memory limit: 128 MB
We are given an arithmetic expression template 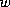 that consists of four basic types of operations,
some brackets and holes, denoted by x, that represent some missing numbers.
For instance, (x*x)/(x+x) is a valid template.
that consists of four basic types of operations,
some brackets and holes, denoted by x, that represent some missing numbers.
For instance, (x*x)/(x+x) is a valid template.
A valuation of a template consists in inserting real numbers to the template so that
the value of the resulting expression is correctly defined.
For instance, by inserting the numbers 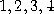 into the respective holes in the example above, we obtain
an expression that evaluates to
into the respective holes in the example above, we obtain
an expression that evaluates to 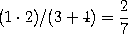 , whereas inserting
the numbers
, whereas inserting
the numbers 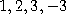 yields an expression with undefined value, hence
this is not a valuation.
yields an expression with undefined value, hence
this is not a valuation.
If the sets of valuations of two templates 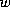 and
and 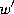 are the same
and for each valuation the expressions obtained from
are the same
and for each valuation the expressions obtained from 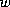 and
and 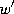 have the same value, and the template
have the same value, and the template 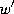 can be obtained by inserting
and/or deleting some brackets from the template
can be obtained by inserting
and/or deleting some brackets from the template 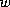 , we say that
the two templates are equivalent.
For instance, the templates (x*x)/(x+x) and x*x/(x+x) are equivalent.
On the other hand, the templates (x*x)/(x+x) and x*x/x+x are not equivalent,
since the valuation
, we say that
the two templates are equivalent.
For instance, the templates (x*x)/(x+x) and x*x/(x+x) are equivalent.
On the other hand, the templates (x*x)/(x+x) and x*x/x+x are not equivalent,
since the valuation 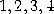 of these templates yields two expressions that
are evaluated to
of these templates yields two expressions that
are evaluated to  and
and 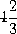 respectively.
Also the templates x-(x-x) and x-x+x are not equivalent
since none of them can be transformed to the other by inserting or removing brackets.
respectively.
Also the templates x-(x-x) and x-x+x are not equivalent
since none of them can be transformed to the other by inserting or removing brackets.
Your task is to find a template with the minimum number of brackets among templates equivalent to a given template.
Multiplication and division have the same priority, which is greater than the priority of addition and subtraction. Hence, multiplication and division are performed before addition and subtraction. Addition and subtraction have the same priority. Operations with the same priority are performed from left to right.
Input
The first line of input contains an integer  that represents the number of expression templates in the input.
Each of the following
that represents the number of expression templates in the input.
Each of the following  lines contains a non-empty, correct expression template consisting of
the characters +, -, *, /, (, ) and x (the holes).
The sum of lengths of all the expressions does not exceed
lines contains a non-empty, correct expression template consisting of
the characters +, -, *, /, (, ) and x (the holes).
The sum of lengths of all the expressions does not exceed 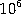 .
.
Output
Your program should output  lines.
The
lines.
The 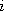 -th line should contain a template that is equivalent to the
-th line should contain a template that is equivalent to the 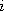 -th template from the input,
which contains the minimum number of brackets.
-th template from the input,
which contains the minimum number of brackets.
Example
For the input data:
2 x+(x+(x+x)-(x*x))/x (x*x)/((x*x))+(x)
the correct result is:
x+(x+x+x-x*x)/x x*x/(x*x)+x
Task author: Tomasz Idziaszek.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English