
Zadanie Łamane płaskie (lam)
Pomóż nam usprawnić bazę zadań!
Łamane płaskie
Limit pamięci: 32 MB
Rozważmy kartezjański układ współrzędnych narysowany na kartce papieru.
Łamaną płaską w tym układzie nazywamy łamaną, którą można wykreślić prowadząc ołówek bez odrywania od papieru w kierunku od lewej do prawej strony kartki i taką,
że każda prosta zawierająca odcinek łamanej jest nachylona do osi 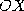 pod kątem należącym do przedziału domkniętego
pod kątem należącym do przedziału domkniętego 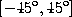 .
.
Na kartce narysowano  różnych punktów o obu współrzędnych całkowitych.
Jaka jest najmniejsza liczba łamanych płaskich, które należałoby wykreślić, żeby każdy z n punktów należał do co najmniej jednej z nich?
różnych punktów o obu współrzędnych całkowitych.
Jaka jest najmniejsza liczba łamanych płaskich, które należałoby wykreślić, żeby każdy z n punktów należał do co najmniej jednej z nich?
Przykład
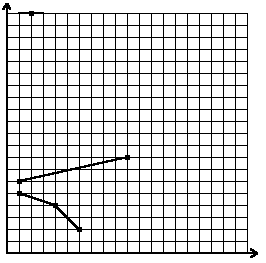
Dla 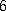 punktów o współrzędnych
punktów o współrzędnych 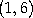 ,
, 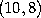 ,
, 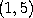 ,
, 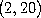 ,
, 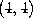 ,
, 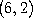 najmniejszą liczbą łamanych płaskich pokrywających te punkty jest
najmniejszą liczbą łamanych płaskich pokrywających te punkty jest 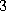 .
.
Zadanie
Napisz program, który:
- wczytuje ze standardowego wejścia liczbę punktów i ich współrzędne;
- oblicza najmniejszą liczbę łamanych płaskich, które należałoby wykreślić, żeby pokryły one wszystkie punkty;
- zapisuje wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia znajduje się dodatnia liczba całkowita  nie większa od
nie większa od 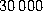 .
Jest to liczba punktów.
W kolejnych
.
Jest to liczba punktów.
W kolejnych  wierszach znajdują się współrzędne punktów.
Każdy wiersz zawiera dwie liczby całkowite
wierszach znajdują się współrzędne punktów.
Każdy wiersz zawiera dwie liczby całkowite 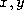 oddzielone pojedynczym odstępem,
oddzielone pojedynczym odstępem,  ,
, 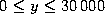 .
Liczby w wierszu
.
Liczby w wierszu 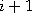 ,
, 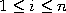 , są współrzędnymi
, są współrzędnymi 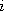 -tego punktu.
-tego punktu.
Wyjście
Twój program powinien zapisać jedną liczbę całkowitą w pierwszym i jedynym wierszu standardowego wyjścia. Tą liczbą powinna być najmniejsza liczba łamanych płaskich, które należy wykreślić, żeby pokryć wszystkie dane punkty.
Przykład
Dla danych wejściowych:
6 1 6 10 8 1 5 2 20 4 4 6 2
poprawną odpowiedzią jest:
3
Autor zadania: Krzysztof Sobusiak.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English