
Zadanie Szachy (ach)
Pomóż nam usprawnić bazę zadań!
Szachy
Limit pamięci: 32 MB
Bajtazar zapukał do drzwi Bajtoniego dokładnie o 17. Bardziej z przyzwyczajenia niż z konieczności, gdyż Bajtoni dobrze znał punktualność przyjaciela i właśnie miał otwierać drzwi.
Po wypiciu gorącej herbaty Bajtoni przyniósł szachownicę, by rozegrać umówioną wcześniej partię szachów, jednak Bajtazar stwierdził, że gry z doskonałą informacją są mało rozwijające i warto inaczej spędzić czas. Bajtoni musiał przyznać mu rację, nie będąc w stanie znaleźć odpowiednich argumentów przeciwko jego opinii. Znalezienie ciekawej rozrywki intelektualnej, którą jeszcze się nie zajmowali, nie trwało krótko, jednak w końcu przyjaciele zdecydowali się rozwiązać następujący problem.
Dana jest szachownica rozmiaru 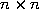 .
Na ile sposobów można ustawić na niej
.
Na ile sposobów można ustawić na niej  wież, tak by w każdym wierszu i w każdej kolumnie znajdowała się co najwyżej jedna figura oraz by po obróceniu szachownicy o
wież, tak by w każdym wierszu i w każdej kolumnie znajdowała się co najwyżej jedna figura oraz by po obróceniu szachownicy o 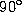 (w płaszczyźnie poziomej) rozstawienie wież wyglądało identycznie?
Pokolorowanie pól na szachownicy po wykonaniu obrotu może się zmienić, jednak nie jest to istotne.
(w płaszczyźnie poziomej) rozstawienie wież wyglądało identycznie?
Pokolorowanie pól na szachownicy po wykonaniu obrotu może się zmienić, jednak nie jest to istotne.
Wejście
W pierwszym i jedynym wierszu standardowego wejścia znajduje się liczba całkowita  (
(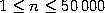 ).
).
Wyjście
Na standardowe wyjście należy wypisać jedną liczbę całkowitą - liczbę różnych rozstawień  wież na szachownicy
rozmiaru
wież na szachownicy
rozmiaru 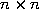 takich, że w każdej kolumnie i każdym wierszu znajduje się co najwyżej jedna wieża
oraz że rozstawienie nie zmienia się po obrocie szachownicy o
takich, że w każdej kolumnie i każdym wierszu znajduje się co najwyżej jedna wieża
oraz że rozstawienie nie zmienia się po obrocie szachownicy o 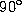 .
.
Przykład
Dla danych wejściowych:
1
poprawną odpowiedzią jest:
1
Autor zadania: Łukasz Bieniasz-Krzywiec.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English