
Zadanie Koza [A] (koz)
Pomóż nam usprawnić bazę zadań!
The Goat [A]
Memory limit: 256 MB
Farmer Byteman took his sledgehammer and drove  stakes into the ground of an infinite pasture.
Through the next
stakes into the ground of an infinite pasture.
Through the next 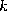 days each morning farmer Byteman takes his goat out to the pasture and ties it to a randomly selected stake with a cord of length
days each morning farmer Byteman takes his goat out to the pasture and ties it to a randomly selected stake with a cord of length 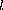 .
During the day the goat eats all the grass in its reach.
To the chargin of the goat the grass does not grow back.
Moreover, it can happen that the scatterbrained farmer will tie the goat more than once to the same stake.
.
During the day the goat eats all the grass in its reach.
To the chargin of the goat the grass does not grow back.
Moreover, it can happen that the scatterbrained farmer will tie the goat more than once to the same stake.
What is the expected value of the area of the pasture on which the grass will be eaten after 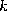 days?
days?
Input
In the first line of the standard input contains three integers  ,
, 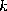 and
and 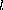 (
(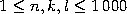 )
denoting respectively the number of stakes, the number of days, and the length of the cord.
Each of the next
)
denoting respectively the number of stakes, the number of days, and the length of the cord.
Each of the next  lines contains the coordinates of one stake in the form of a pair of integers
lines contains the coordinates of one stake in the form of a pair of integers 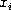 ,
, 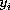 (
(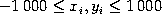 ).
No two stakes are driven into the ground in the same place.
).
No two stakes are driven into the ground in the same place.
Output
In the only line of the standard output a single real number should be written.
The number should be the expected value of the area of the part of the pasture from which the goat will have eaten the grass during 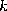 days.
The answer will be accepted if it will differ from the correct answer by no more than
days.
The answer will be accepted if it will differ from the correct answer by no more than 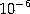 .
No more than
.
No more than 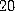 digits should be given after the decimal point.
digits should be given after the decimal point.
Example
For the input data:
2 2 1 0 0 1 0
the correct result is:
4.098204131080311
Explanation of the example:
If the goat will be tied to the same stake during both days the area of the eaten grass will be equal to  . On the other hand if it will be tied to two different stakes, the area will be equal to
. On the other hand if it will be tied to two different stakes, the area will be equal to 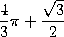 .
Thus the answer is
.
Thus the answer is 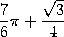 .
.
Task author: Tomasz Idziaszek.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English