
Zadanie Dwa tartaki (two)
Pomóż nam usprawnić bazę zadań!
Two Sawmills
Memory limit: 32 MB
There are  old trees planted along a road that goes from the
top of a hill to its bottom.
Local government decided to cut them down.
In order not to waste wood each tree should be transported
to a sawmill.
old trees planted along a road that goes from the
top of a hill to its bottom.
Local government decided to cut them down.
In order not to waste wood each tree should be transported
to a sawmill.
Trees can be transported only in one direction: downwards. There is a sawmill at the lower end of the road. Two additional sawmills can be built along the road. You have to decide where to build them, as to minimize the cost of transportation. The transportation costs one cent per meter, per kilogram of wood.
Task
Write a program, that:
- reads from the standard input the number of trees, their weights and locations,
- calculates the minimum cost of transportation,
- writes the result to the standard output.
Input
The first line of the input contains one integer  -
the number of trees (
-
the number of trees (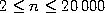 ).
The trees are numbered
).
The trees are numbered 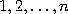 , starting from the top
of the hill and going downwards.
Each of the following
, starting from the top
of the hill and going downwards.
Each of the following  lines contains two positive integers
separated by single space.
Line
lines contains two positive integers
separated by single space.
Line 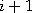 contains:
contains:
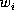 - weight (in kilograms) of the
- weight (in kilograms) of the 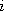 -th tree and
-th tree and
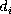 - distance (in meters) between trees number
- distance (in meters) between trees number 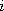 and
and 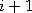 ,
,
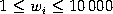 ,
, 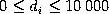 .
The last of these numbers,
.
The last of these numbers, 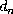 , is the distance from
the tree number
, is the distance from
the tree number  to the lower end of the road.
It is guaranteed that the total cost of transporting all trees
to the sawmill at the end of the road is less than
to the lower end of the road.
It is guaranteed that the total cost of transporting all trees
to the sawmill at the end of the road is less than 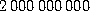 cents.
cents.
Output
The first and only line of output should contain one integer: the minimum cost of transportation.
Example
For the input data:
9 1 2 2 1 3 3 1 1 3 2 1 6 2 1 1 2 1 1
the correct result is:
26

The figure shows the optimal location of sawmills for the example data.
Trees are depicted as circles with weights given below.
Sawmills are marked black.
The result is equal to:
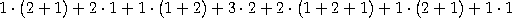 .
.
Task author: Wojciech Rytter.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English