
Zadanie Sieć dróg (sie)
Pomóż nam usprawnić bazę zadań!
Sieć dróg
Limit pamięci: 32 MB
Do mapy drogowej dołączona została dyskietka z tabelą długości najkrótszych dróg (odległości) między każdymi dwoma miastami na mapie.
Wszystkie drogi są dwukierunkowe.
Położenie miast na mapie ma następującą ciekawą własność.
Jeżeli długość najkrótszej drogi z miasta 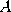 do
do 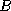 jest równa sumie długości najkrótszych dróg z
jest równa sumie długości najkrótszych dróg z 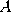 do
do 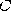 i z
i z 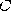 do
do 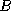 ,
to miasto
,
to miasto 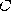 leży na (pewnej) najkrótszej drodze z
leży na (pewnej) najkrótszej drodze z 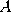 do
do 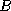 .
Powiemy, że dwa miasta
.
Powiemy, że dwa miasta 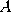 i
i 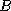 sąsiadują ze sobą, jeżeli nie istnieje miasto
sąsiadują ze sobą, jeżeli nie istnieje miasto 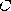 takie,
że długość najkrótszej drogi z miasta
takie,
że długość najkrótszej drogi z miasta 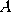 do
do 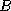 jest równa długości najkrótszych dróg z
jest równa długości najkrótszych dróg z 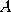 do
do 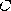 i z
i z 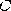 do
do 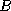 .
.
Na podstawie danej tabeli odległości znajdź wszystkie pary miast sąsiadujących ze sobą.
Przykład
Jeżeli tabela odległości ma postać
A B C A 0 1 2 B 1 0 3 C 2 3 0
wówczas sąsiednimi miastami są 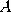 i
i 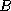 oraz
oraz 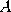 i
i 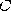 .
.
Zadanie
Napisz program, który:
- wczytuje ze standardowego wejścia tabele odległości;
- znajduje wszystkie pary sąsiednich miast;
- zapisuje wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia znajduje się liczba całkowita  ,
, 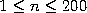 .
Jest to liczba miast na mapie.
Miasta ponumerowane są jednoznacznie od
.
Jest to liczba miast na mapie.
Miasta ponumerowane są jednoznacznie od 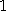 do
do  .
.
Tabela odległości jest zapisana w kolejnych  wierszach.
W wierszu
wierszach.
W wierszu 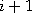 ,
, 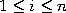 , jest zapisanych
, jest zapisanych  nieujemnych liczb całkowitych nie większych od
nieujemnych liczb całkowitych nie większych od 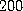 , oddzielonych pojedynczym odstępem.
Liczba
, oddzielonych pojedynczym odstępem.
Liczba 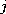 -ta jest odległości między miastami
-ta jest odległości między miastami 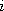 oraz
oraz 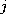 .
.
Wyjście
Twój program powinien wypisać na standardowe wyjście wszystkie pary (numerów) sąsiednich miast, po jednej parze w każdym wierszu.
Każda para powinna pojawia się tylko raz.
Liczby w parze powinny być uporządkowane rosnąco i oddzielone pojedynczym odstępem.
Kolejność wypisywania par powinna być taka, że dla pary 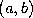 poprzedzającej parę
poprzedzającej parę 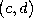 ,
, 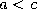 lub (
lub ( i
i 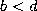 ).
).
Przykład
Dla danych wejściowych:
3 0 1 2 1 0 3 2 3 0
poprawną odpowiedzią jest:
1 2 1 3
Autor zadania: Piotr Chrząstowski-Wachtel.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English