
Zadanie Odległość (odl)
Pomóż nam usprawnić bazę zadań!
Odległość
Limit pamięci: 128 MB
W tym zadaniu rozważamy odległość między dodatnimi liczbami całkowitymi, zdefiniowaną w następujący sposób.
Przez pojedynczą operację rozumiemy pomnożenie danej liczby przez liczbę pierwszą1
lub podzielenie jej przez liczbę pierwszą (o ile dzieli się ona bez reszty).
Odległość między liczbami  i
i 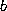 , oznaczana
, oznaczana 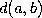 , to minimalna liczba operacji potrzebnych
do przekształcenia liczby
, to minimalna liczba operacji potrzebnych
do przekształcenia liczby  w liczbę
w liczbę 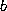 .
Na przykład,
.
Na przykład, 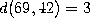 .
.
Zauważmy, że faktycznie funkcja  ma cechy odległości - dla dowolnych dodatnich
liczb całkowitych
ma cechy odległości - dla dowolnych dodatnich
liczb całkowitych  ,
, 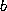 i
i  zachodzi:
zachodzi:
-
odległość liczby od niej samej wynosi 0:
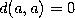 ,
,
-
odległość od
 do
do 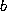 jest taka sama, jak od
jest taka sama, jak od 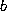 do
do  :
: 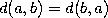 , oraz
, oraz
-
spełniona jest nierówność trójkąta:
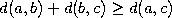 .
.
 dodatnich liczb całkowitych
dodatnich liczb całkowitych 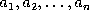 .
Dla każdej liczby
.
Dla każdej liczby 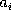 należy wskazać takie
należy wskazać takie 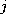 , że
, że 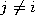 oraz
oraz 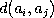 jest minimalne.
jest minimalne.
Wejście
W pierwszym wierszu standardowego wejścia znajduje się jedna liczba całkowita  (
(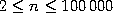 ).
W kolejnych wierszach znajdują się liczby
).
W kolejnych wierszach znajdują się liczby 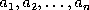 (
(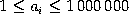 ),
po jednej w wierszu.
),
po jednej w wierszu.
W testach wartych łącznie 30% punktów zachodzi dodatkowy warunek 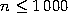 .
.
Wyjście
Twój program powinien wypisać na standardowe wyjście dokładnie  wierszy, a w każdym z nich po jednej liczbie całkowitej.
W
wierszy, a w każdym z nich po jednej liczbie całkowitej.
W 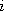 -tym wierszu należy wypisać najmniejsze takie
-tym wierszu należy wypisać najmniejsze takie 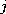 , że:
, że: 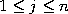 ,
, 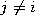 oraz
oraz 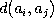 jest minimalne.
jest minimalne.
Przykład
Dla danych wejściowych:
6 1 2 3 4 5 6
poprawną odpowiedzią jest:
2 1 1 2 1 2
Autor zadania: Wojciech Śmietanka.
1. Przypomnijmy, że liczba pierwsza to taka liczba całkowita dodatnia, która ma dokładnie dwa różne dzielniki: jedynkę i siebie samą.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English