
Zadanie Ewaluacja (ewa)
Pomóż nam usprawnić bazę zadań!
Evaluation of an Expression
Memory limit: 128 MB
Consider an expression 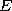 , containing
integer constants from 0 to 9, variables from
, containing
integer constants from 0 to 9, variables from  to
to  ,
and the following operations: addition, multiplication and exponentiation
with a constant exponent.
Quite surprisingly, each of the variables
,
and the following operations: addition, multiplication and exponentiation
with a constant exponent.
Quite surprisingly, each of the variables 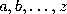 appears in the expression
appears in the expression 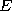 at most once.
For a given prime number
at most once.
For a given prime number 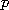 , we would like to know how many roots modulo
, we would like to know how many roots modulo 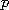 the polynomial represented by this expression has.
In other words, we want to count the number of ways in which integers from
the polynomial represented by this expression has.
In other words, we want to count the number of ways in which integers from 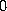 to
to
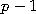 can be assigned to the variables in
can be assigned to the variables in 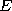 , so that the value of
, so that the value of 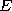 is divisible by
is divisible by 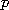 .
Since the number of such roots can turn out large, it suffices to output it
modulo
.
Since the number of such roots can turn out large, it suffices to output it
modulo 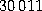 .
.
For example, the polynomial represented by the following expression:
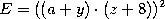
has 15 roots modulo 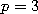 , among which the roots:
, among which the roots:
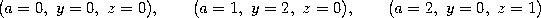
can be found.
More formally, an expression is defined as follows:
- Each integer constant 0, 1, ..., 9 is an expression.
- Each variable a, b, ..., z is an expression.
- If A and B are any expressions, then each of (A+B) and (A*B) is also an expression: the first is the sum of expressions A and B, and the second is their product.
- If A is any expression, and B is an integer constant from 2, 3, ..., 9, then (A^B) is also an expression: the expression A raised to the power of B.
Input
The first line of input contains one prime number 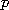 (
(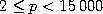 ).
The second line contains an expression
).
The second line contains an expression 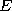 as specified above, described
by a sequence of at most 300 characters
0, 1, ..., 9, a, b, ..., z,
+, *, ^,
(, ),
without any white space.
as specified above, described
by a sequence of at most 300 characters
0, 1, ..., 9, a, b, ..., z,
+, *, ^,
(, ),
without any white space.
Output
Let 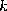 denote the number of roots modulo
denote the number of roots modulo 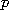 of the polynomial
of the polynomial 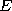 .
Your program should output one non-negative integer,
.
Your program should output one non-negative integer, 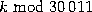 .
.
Example
For the input data:
3 (((a+y)*(z+8))^2)
the correct result is:
15
Task author: Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English