
Zadanie Obchodzenie drzewa skokami (obc)
Pomóż nam usprawnić bazę zadań!
Step Traversing a Tree
Memory limit: 32 MB
A graph is a pair 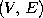 , where
, where 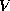 is a finite set of
elements called vertices of the graph, and
is a finite set of
elements called vertices of the graph, and 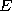 is a subset of the set
of all unordered pairs of distinct vertices. The elements of the set
is a subset of the set
of all unordered pairs of distinct vertices. The elements of the set
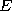 are called edges of the graph. If for each pair of distinct
vertices
are called edges of the graph. If for each pair of distinct
vertices  ,
,  there exists exactly one sequence of
distinct vertices
there exists exactly one sequence of
distinct vertices 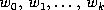 , such that
, such that
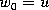 ,
,  and the pairs
and the pairs 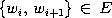 for
for 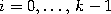 , then the graph is
called a tree. We say that the distance between the vertices
, then the graph is
called a tree. We say that the distance between the vertices  and
and
 in the tree is
in the tree is 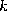 .
.
It is known that a tree of  vertices has exactly
vertices has exactly 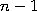 edges. A tree
edges. A tree 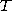 whose vertices are numbered from
whose vertices are numbered from 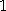 to
to
 can be unambiguously described by giving the number of its vertices
can be unambiguously described by giving the number of its vertices
 , and an appropriate sequence of
, and an appropriate sequence of 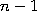 pairs of positive
integers describing its edges.
pairs of positive
integers describing its edges.
Any permutation of vertices - i.e. a sequence in which each vertex appears
exactly once - is called a traversing order of a tree. If the distance of each
two consecutive vertices in some order of the tree  is at most
is at most
 , then we say that it is a traversing order of the tree with step
, then we say that it is a traversing order of the tree with step
 .
.
It is known that for each tree its traversing order with step 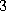 can
be found.
can
be found.
Example
The picture shows a tree of 7 vertices. The vertices are represented by black dots, and edges by line segments joining the dots.
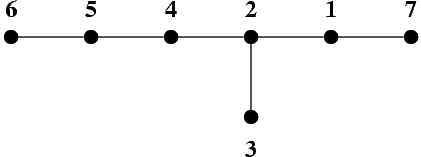
This tree can be traversed with step 3 by visiting its vertices in the following order: 7 2 3 5 6 4 1.
Task
Write a program that:
- reads a description of a tree from the standard input.
- finds an arbitrary traversing order of that tree with step
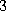 ,
, - writes that order in the standard output.
Input
- In the first line of the standard input there is a positive integer
 , not greater than
, not greater than 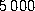 - it is the number of vertices
of the tree.
- it is the number of vertices
of the tree. - In each of the following
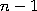 lines there is one pair of positive
integers separated by a single space and representing one edge of the tree.
lines there is one pair of positive
integers separated by a single space and representing one edge of the tree.
Output
In the successive lines of the standard output one should write the numbers of the successive vertices in a traversing order of the tree with step 3 - each number should be written in a separate line.
Example
For the input data:
7 1 2 2 3 2 4 4 5 5 6 1 7
the correct result is:
7 2 3 5 6 4 1
Task author: Krzysztof Diks.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English