
Zadanie Video poker [A] (vid)
Pomóż nam usprawnić bazę zadań!
Video Poker [A]
Limit pamięci: 32 MB
Bajtazar wybrał się na wakacje do Bajt Vegas. W stolicy hazardu najbardziej polubił grę w Video Pokera. Ponieważ jest to gra wymagająca przemyślanej strategii, Bajtazar postanowił zamówić u Ciebie program, który pomoże mu dobrze w nią grać.
Do gry w Video Pokera wykorzystywana jest zwykła talia 52 kart (od dwójki do asa, cztery kolory). Gra jest przeznaczona dla jednego gracza, który za rozdanie płaci jedną stawkę. Gracz otrzymuje pięć losowych kart z talii. Następnie, wedle własnego uznania, część z nich zatrzymuje, a pozostałe wymienia. Wymieniane karty są odrzucane i na ich miejsce gracz dostaje nowe karty z talii. Ostatecznie gracz otrzymuje wypłatę określoną przez kasyno w tabeli wypłat, zależnie od tego, jaki układ pokerowy udało mu się uzyskać.
Rozróżniane są następujące układy (od najsłabszego do najsilniejszego):
- Para - dwie karty o tej samej wartości. Aby otrzymać wypłatę za parę, musi to być para waletów, dam, króli lub asów.
- Dwie pary - dwie pary (dowolnej wartości).
- Trójka - trzy karty o tej samej wartości.
- Strit - pięć kart o kolejnych wartościach. As może być częścią strita jako karta starsza od króla lub młodsza od dwójki, ale nie w obydwu tych znaczeniach naraz.
- Kolor - pięć kart tego samego koloru.
- Full - trzy karty o tej samej wartości oraz para o innej wartości.
- Kareta - cztery karty o tej samej wartości.
- Poker - strit i kolor jednocześnie.
- Poker królewski - poker złożony z asa, króla, damy, waleta i dziesiątki.
Gracz otrzymuje wypłatę jedynie za najsilniejszy układ jaki posiada (jeśli np. ma fulla, to ma też oczywiście trójkę, jednak wypłata jest równa wartości fulla w tabeli wypłat). Jeśli graczowi nie udaje się uzyskać żadnego z powyższych układów, nie otrzymuje wypłaty.
Bajtazar chciałby wiedzieć jaka jest optymalna (maksymalizująca wartość oczekiwaną wypłaty) strategia w różnych kasynach, różniących się tabelami wypłat. Udowodnij Bajtazarowi, że umiesz obliczyć tę strategię! Dla każdej tabeli wypłat policz dla ilu przypadków rozdanych pięciu kart grając strategią optymalną zatrzymasz wszystkie karty, dla ilu odrzucisz jedną, ilu dwie, trzy, cztery i wreszcie wszystkie pięć kart. Jeśli kilka ruchów może dać tę samą wartość oczekiwaną, należy wybrać ten z nich, w którym zachowuje się najmniejszą liczbę kart.
Bajtazar podał Ci z góry jakie są tabele wypłat w interesujących go kasynach. Twój program może po prostu wypisywać obliczone wcześniej wartości.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia tabelę wypłat za poszczególne układy,
- wypisze na standardowe wyjście liczbę rozdań, w których grając optymalnie odrzuca się odpowiednio 0, 1, 2, 3, 4 i 5 kart.
Wejście
Pierwszy i jedyny wiersz wejścia określa tabelę wypłat. Zawiera on dziewięć liczb całkowitych dodatnich, pooddzielanych pojedynczymi odstępami. Są to kolejno wypłaty za parę, dwie pary, trójkę, strita, kolor, fulla, karetę, pokera i pokera królewskiego. Twój program zostanie przetestowany dla następujących danych:
-
1 2 3 4 6 9 25 50 940
-
1 2 3 4 5 9 25 50 800
-
1 2 3 4 6 8 25 50 800
-
1 2 3 4 5 8 25 50 800
-
1 2 3 4 5 7 25 50 800
-
1 2 3 4 5 6 25 50 800
-
1 2 2 4 6 9 30 125 1000
-
1 2 2 4 6 9 30 100 1000
-
1 2 3 4 5 6 25 50 1000
-
1 2 2 4 6 9 30 100 500
Wyjście
Na wyjściu powinno zostać wypisanych dokładnie 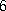 liczb całkowitych w jednym wierszu,
pooddzielanych pojedynczymi odstępami. Mają one określać kolejno liczby rozdań, w których
grając optymalnie odrzuca się
liczb całkowitych w jednym wierszu,
pooddzielanych pojedynczymi odstępami. Mają one określać kolejno liczby rozdań, w których
grając optymalnie odrzuca się 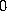 ,
, 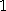 ,
, 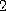 ,
, 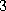 ,
,  i
i 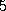 kart.
kart.
Przykład
Dla danych wejściowych:1 2 3 4 6 9 25 50 800poprawną odpowiedzią jest:
18864 292800 147528 1651440 403968 84360
Autor zadania: Marek Turski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English