
Zadanie Loteria 2 (lod)
Pomóż nam usprawnić bazę zadań!
Loteria 2
Limit pamięci: 128 MB
Przedsiębiorstwo Bajtocki Lotek specjalizuje się w przeprowadzaniu gier liczbowych i loterii pieniężnych, wśród których największą popularnością cieszy się loteria o nazwie Gra w liczby. Również Bajtazar postanowił spróbować szczęścia w grze.
Kupon do Gry w liczby zawiera  pozycji.
Na każdej z nich można zakreślić jedną z liczb
pozycji.
Na każdej z nich można zakreślić jedną z liczb 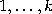 .
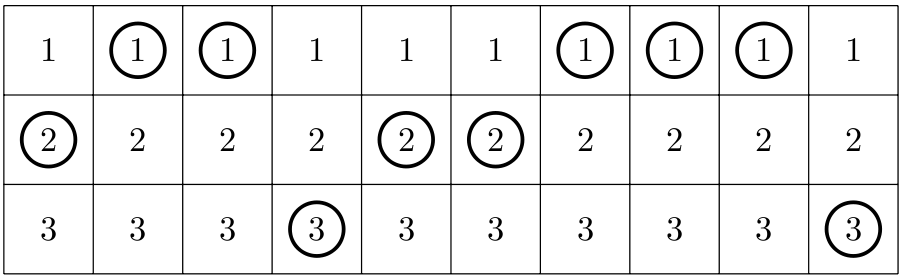
Poniższy rysunek przedstawia przykładowe wypełnienie kuponu dla
.
Poniższy rysunek przedstawia przykładowe wypełnienie kuponu dla  i
i  :
:
Losowanie zwycięzców przeprowadza się przy pomocy maszyny losującej, w której
znajduje się po  kulek każdego z rodzajów
kulek każdego z rodzajów 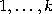 , co daje łącznie
, co daje łącznie 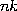 kulek.
W górnej części maszyny jest rozmieszczonych równomiernie
kulek.
W górnej części maszyny jest rozmieszczonych równomiernie  otworów o średnicy mniejszej
niż średnica kulki.
W pewnym momencie losowania włączany jest mechanizm pneumatyczny, który powoduje, że
do każdego z otworów przyssana zostaje jedna kulka.
Wypisując kolejno liczby znajdujące się na wylosowanych kulkach, otrzymuje się
ciąg złożony z
otworów o średnicy mniejszej
niż średnica kulki.
W pewnym momencie losowania włączany jest mechanizm pneumatyczny, który powoduje, że
do każdego z otworów przyssana zostaje jedna kulka.
Wypisując kolejno liczby znajdujące się na wylosowanych kulkach, otrzymuje się
ciąg złożony z  liczb, stanowiący wynik losowania.
Szczęśliwi właściciele kuponów, na których zakreślono taki właśnie ciąg liczb,
zdobywają nagrodę główną - milion bajtalarów do podziału.
Na rysunku przedstawiono wynik losowania, przy którym powyższy kupon uzyskałby główną nagrodę.
liczb, stanowiący wynik losowania.
Szczęśliwi właściciele kuponów, na których zakreślono taki właśnie ciąg liczb,
zdobywają nagrodę główną - milion bajtalarów do podziału.
Na rysunku przedstawiono wynik losowania, przy którym powyższy kupon uzyskałby główną nagrodę.

Bajtazar nabył kupon i zakreślił na nim  liczb.
Zanim jednak zdążył złożyć swój kupon w kolekturze, w mediach pojawił
się przeciek, że losowanie w Grze w liczby nie jest do końca uczciwe.
Zbadano bowiem, że kulki tego samego rodzaju - czyli z tą samą liczbą -
odpychają się i nigdy nie ustawią się przy sąsiednich otworach
w trakcie losowania (np. układ kulek przedstawiony na powyższym rysunku nie byłby możliwy).
liczb.
Zanim jednak zdążył złożyć swój kupon w kolekturze, w mediach pojawił
się przeciek, że losowanie w Grze w liczby nie jest do końca uczciwe.
Zbadano bowiem, że kulki tego samego rodzaju - czyli z tą samą liczbą -
odpychają się i nigdy nie ustawią się przy sąsiednich otworach
w trakcie losowania (np. układ kulek przedstawiony na powyższym rysunku nie byłby możliwy).
Bajtazar, dowiedziawszy się o tym, postanowił zmienić ciąg  liczb, który wskazał,
tak aby żadne dwie kolejne liczby w ciągu nie były takie same.
Żeby nie kusić losu, chciałby zmienić możliwie najmniej liczb w swoim ciągu.
Pomóż Bajtazarowi ustalić, ile liczb musi zmienić.
liczb, który wskazał,
tak aby żadne dwie kolejne liczby w ciągu nie były takie same.
Żeby nie kusić losu, chciałby zmienić możliwie najmniej liczb w swoim ciągu.
Pomóż Bajtazarowi ustalić, ile liczb musi zmienić.
Wejście
Pierwszy wiersz wejścia zawiera dwie liczby całkowite  oraz
oraz 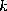 (
(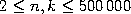 ).
Drugi wiersz zawiera ciąg
).
Drugi wiersz zawiera ciąg  liczb z zakresu
liczb z zakresu  .
W ciągu tym występuje co najmniej jedna para sąsiadujących ze sobą takich samych liczb.
.
W ciągu tym występuje co najmniej jedna para sąsiadujących ze sobą takich samych liczb.
Wyjście
Pierwszy i jedyny wiersz wyjścia powinien zawierać jedną liczbę całkowitą dodatnią - minimalną liczbę liczb w ciągu, które trzeba zmienić, tak aby żadne dwie takie same liczby nie występowały w nim obok siebie.
Przykład
Dla danych wejściowych:
10 3 2 1 1 3 2 2 1 1 1 3
poprawną odpowiedzią jest:
3
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English