
Zadanie Gra (gra)
Pomóż nam usprawnić bazę zadań!
Gra
Limit pamięci: 32 MB
Plansza do gry składa się z 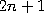 kolejno ponumerowanych pól.
Na planszy znajduje się
kolejno ponumerowanych pól.
Na planszy znajduje się  czarnych pionków i
czarnych pionków i  białych.
Czarne pionki są rozmieszczone na
białych.
Czarne pionki są rozmieszczone na  początkowych polach planszy (na polach o numerach
od 1 do
początkowych polach planszy (na polach o numerach
od 1 do  ), natomiast białe na
), natomiast białe na  końcowych polach (na polach o numerach od
końcowych polach (na polach o numerach od 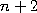 do
do 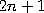 ).
Pole o numerze
).
Pole o numerze 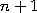 jest początkowo wolne.
jest początkowo wolne.
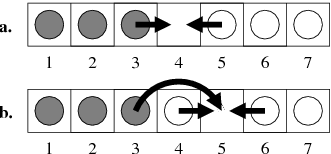
a. początkowe ustawienie pionków na planszy dla 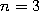 i możliwe ruchy,
i możliwe ruchy,
b. plansza po wykonaniu ruchu pionkiem z pola 5 i możliwe ruchy
Na planszy można wykonywać dwa rodzaje ruchów polegających na przesunięciu pionka na sąsiednie wolne pole, albo na przeskoczeniu pionkiem nad sąsiednim pionkiem odmiennego koloru i wylądowaniu na wolnym polu.
Celem gry jest zamiana miejscami pionków czarnych i białych (tzn. rozmieszczenie czarnych pionków
na polach o numerach od 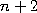 do
do 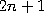 , a białych na polach o numerach od 1 do
, a białych na polach o numerach od 1 do  ).
Interesuje nas najkrótszy ciąg dozwolonych wyników wystarczających do zreazlizowania tego celu.
).
Interesuje nas najkrótszy ciąg dozwolonych wyników wystarczających do zreazlizowania tego celu.
Zadanie
Napisz program, który:
-
wczyta liczbę
 oznaczającą liczbę czarnych pionków na planszy,
oznaczającą liczbę czarnych pionków na planszy,
- wyznaczy najkrótszy ciąg ruchów realizującą cel gry,
- wypisze wynik.
Wejście
W jedynym wierszu wejścia znajduje się liczba całkowita  (
(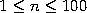 ).
).
Wyjście
W pierwszym wierszu wyjścia należy wypisać liczbę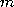 oznaczająca minimalną liczbę ruchów wystarczających do tego,
aby doprowadzić pionki na planszy do konfiguracji końcowej. W kolejnych
oznaczająca minimalną liczbę ruchów wystarczających do tego,
aby doprowadzić pionki na planszy do konfiguracji końcowej. W kolejnych 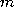 wierszach należy zapisać po jednej liczbie
z przedziału
wierszach należy zapisać po jednej liczbie
z przedziału 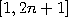 .
Liczba znajdująca się w
.
Liczba znajdująca się w 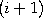 -szym wierszu (dla
-szym wierszu (dla 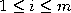 ) oznacza
numer pola, z którego należy przesunąć pionek w
) oznacza
numer pola, z którego należy przesunąć pionek w 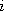 -tym ruchu.
-tym ruchu.
Jeśli istnieje więcej niż jedno rozwiązanie, Twój program może wypisać dowolne z nich.
Przykład
Dla danych wejściowych:1poprawną odpowiedzią jest:
3 1 3 2
Autor zadania: Tomasz Idziaszek.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English