Permutation

Memory limit: 32 MB

Multiset is a mathematical object similar to a set, but each member of a multiset may have more than one membership. Just as with any set, the members of a multiset can be ordered in many ways. We call each such ordering a permutation of the multiset. For example, among the permutations of the multiset 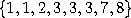there are 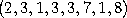and .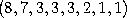

We will say that one permutation of a given multiset is smaller (in lexicographic order) than another permutation, if on the first position that does not match the first permutation has a smaller element than the other one. All permutations of a given multiset can be numbered (starting from one) in an increasing order.

Task

Write a programme that

• reads the description of a permutation of a multiset and a positive integer 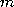from the standard input,
• determines the remainder of the rank of that permutation in the lexicographic ordering modulo ,
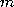• writes out the result to the standard output.

Input

The first line of the standard input holds two integers and 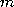(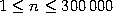, 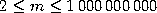), separated by a single space. These denote, respectively, the cardinality of the multiset and \dots\ the number 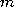. The second line of the standard input contains positive integers 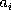(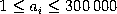), separated by single spaces and denoting successive elements of the multiset permutation.

Output

The first and only line of the standard output is to hold one integer, the remainder modulo 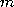of the rank of the input permutation in the lexicographic ordering.

Example

For the input data:

4 1000
2 1 10 2

the correct result is:

5

All the permutations smaller (with respect to lexicographic order) than the one given are: 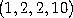, , 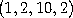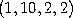and .

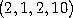Task author: Jakub Radoszewski.