
Zadanie Dzielniki (dzi)
Pomóż nam usprawnić bazę zadań!
Dzielniki
Limit pamięci: 64 MB
W tym zadaniu interesować nas będą dzielniki pewnej liczby naturalnej  .
Oznaczmy zbiór wszystkich tych dzielników przez
.
Oznaczmy zbiór wszystkich tych dzielników przez 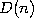 .
Dane jest wyrażenie, składające się ze stałych ze zbioru
.
Dane jest wyrażenie, składające się ze stałych ze zbioru 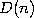 , zmiennych mogących przyjmować
dowolne wartości ze zbioru
, zmiennych mogących przyjmować
dowolne wartości ze zbioru 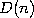 oraz dwuargumentowych funkcji obliczających największy wspólny
dzielnik oraz najmniejszą wspólną wielokrotność.
oraz dwuargumentowych funkcji obliczających największy wspólny
dzielnik oraz najmniejszą wspólną wielokrotność.
Dla podanego wyrażenia należy stwierdzić, czy jego wartość jest stała niezależnie od wartości zmiennych.
Wejście
W pierwszym wierszu standardowego wejścia znajduje się liczba całkowita 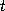 (
(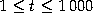 ) oznaczająca liczbę zestawów danych.
W każdym z kolejnych
) oznaczająca liczbę zestawów danych.
W każdym z kolejnych 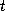 wierszy znajduje się opis jednego zestawu danych.
Każdy taki opis rozpoczyna się liczbą całkowitą
wierszy znajduje się opis jednego zestawu danych.
Każdy taki opis rozpoczyna się liczbą całkowitą 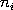 (
(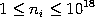 ).
Po niej następuje opis wyrażenia.
Wyrażenie jest stałą, zmienną lub funkcją.
).
Po niej następuje opis wyrażenia.
Wyrażenie jest stałą, zmienną lub funkcją.
Każda liczba w opisie oznacza stałą.
Wszystkie liczby są dodatnimi dzielnikami 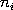 .
.
Zmienne reprezentowane są przez ciągi co najwyżej 5 małych liter alfabetu angielskiego. Utożsamiamy zmienne reprezentowane przez takie same ciągi liter.
Ciągi znaków NWD i NWW oznaczają odpowiednio funkcje zwracające największy wspólny dzielnik oraz najmniejszą wspólną wielokrotność. Po nazwie funkcji następuje pojedynczy odstęp, a po nim oddzielone odstępem opisy dwóch argumentów, które są wyrażeniami (a zatem opis jest rekurencyjny).
Można założyć, że sumaryczny rozmiar pliku wejściowego nie przekroczy 2 MB.
Wyjście
Na standardowe wyjście należy wypisać 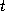 wierszy, zawierających odpowiedzi dla kolejnych zestawów danych.
Odpowiedzią dla jednego zestawu jest słowo TAK lub NIE, w zależności od tego, czy
wyrażenie opisane w zestawie reprezentuje funkcję stałą.
wierszy, zawierających odpowiedzi dla kolejnych zestawów danych.
Odpowiedzią dla jednego zestawu jest słowo TAK lub NIE, w zależności od tego, czy
wyrażenie opisane w zestawie reprezentuje funkcję stałą.
Przykład
Dla danych wejściowych:
3 24 NWD 3 NWW x 12 15 NWD 15 nwd 10 10
poprawną odpowiedzią jest:
TAK NIE TAK
Autor zadania: Dariusz Leniowski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English