
Zadanie Podzbiory [A] (pod)
Pomóż nam usprawnić bazę zadań!
Podzbiory [A]
Limit pamięci: 32 MB
Będziemy rozważać podzbiory 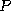 zbioru
zbioru 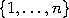 , które
dla danej liczby całkowitej
, które
dla danej liczby całkowitej 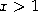 mają własność, że dla każdej
liczby naturalnej
mają własność, że dla każdej
liczby naturalnej 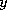 co najmniej jedna z liczb:
co najmniej jedna z liczb: 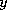 ,
, 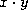 nie należy do
nie należy do 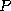 .
Zastanawiamy się, ile jest takich podzbiorów, zawierających dokładnie
.
Zastanawiamy się, ile jest takich podzbiorów, zawierających dokładnie
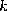 elementów.
Niewykluczone, że wynik jest dość spory - dlatego wystarczy nam
wiedza o reszcie z dzielenia go przez
elementów.
Niewykluczone, że wynik jest dość spory - dlatego wystarczy nam
wiedza o reszcie z dzielenia go przez 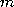 .
.
Zadanie
Napisz program, który:
-
wczyta ze standardowego wejścia cztery liczby całkowite:
 ,
, 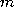 ,
, 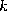 oraz
oraz  ,
,
-
wyznaczy resztę z dzielenia przez
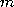 liczby
liczby 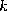 -elementowych
podzbiorów zbioru
-elementowych
podzbiorów zbioru 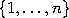 , spełniających wyżej opisaną
własność,
, spełniających wyżej opisaną
własność,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym i jedynym wierszu wejścia znajdują się cztery liczby
całkowite  ,
, 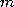 ,
, 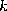 oraz
oraz  (
(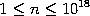 ,
,
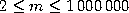 ,
, 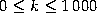 ,
,
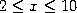 ), pooddzielane pojedynczymi odstępami.
), pooddzielane pojedynczymi odstępami.
Wyjście
Pierwszy i jedyny wierszy wyjścia powinien zawierać jedną
liczbę całkowitą - resztę z dzielenia przez 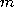 liczby
liczby
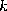 -elementowych podzbiorów zbioru
-elementowych podzbiorów zbioru 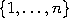 o rozważanej
własności.
o rozważanej
własności.
Przykład
Dla danych wejściowych:6 1234 3 2poprawną odpowiedzią jest:
9
Szukanymi podzbiorami są:
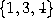 ,
,
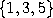 ,
,
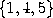 ,
,
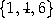 ,
,
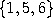 ,
,
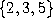 ,
,
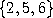 ,
,
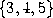 oraz
oraz
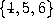 .
.
Autor zadania: Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English