
Zadanie Wielokąty (wie)
Pomóż nam usprawnić bazę zadań!
Wielokąty
Limit pamięci: 32 MB
Mały Jasio na ostatniej lekcji matematyki miał klasówkę z geometrii.
Jedno z najtrudniejszych zadań, jakie Pani dała do rozwiązania było
następujące: Dla danych dwóch trójkątów 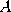 oraz
oraz 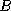 należy wyznaczyć
powierzchnię wielokąta C, który jest zdefiniowany następująco:
należy wyznaczyć
powierzchnię wielokąta C, który jest zdefiniowany następująco: 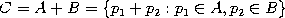 .
Przykładowo, dla dwóch trójkątów:
.
Przykładowo, dla dwóch trójkątów:  o wierzchołkach
o wierzchołkach 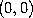 ,
, 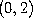 i
i 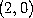 oraz
oraz 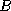 o wierzchołkach
o wierzchołkach 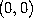 ,
, 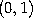 ,
, 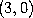 ,
, 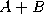 jest wielokątem
o wierzchołkach
jest wielokątem
o wierzchołkach 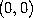 ,
, 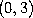 ,
, 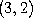 i
i 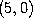 , zatem powierzchnia
, zatem powierzchnia 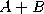 wynosi
wynosi
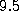 .
.
Jasio po powrocie do domu zaczął się zastanawiać nad tym zadaniem - "Co
należałoby zrobić, aby policzyć powierzchnię 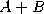 , jeśli
, jeśli 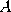 i
i 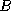 są dowolnymi
wielokątami wypukłymi?". Ponieważ Mały Jasio ma jutro klasówkę z biologii
i musi się do niej przygotować, poprosił Ciebie o pomoc w rozwiązaniu tego
zadania.
są dowolnymi
wielokątami wypukłymi?". Ponieważ Mały Jasio ma jutro klasówkę z biologii
i musi się do niej przygotować, poprosił Ciebie o pomoc w rozwiązaniu tego
zadania.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia opis dwóch wielokątów wypukłych
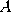 i
i 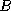 ,
,
- wyznaczy powierzchnię
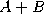 ,
,
- wypisze ją podwojoną na standardowe wyjście.
Wejście
Pierwszy wiersz wejścia zawiera dwie liczby całkowite  i
i 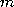 (
(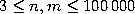 ), oznaczające odpowiednio liczbę wierzchołków wielokątów
), oznaczające odpowiednio liczbę wierzchołków wielokątów
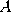 i
i 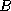 . W drugiej linii wejścia znajduje się
. W drugiej linii wejścia znajduje się  par liczb
całkowitych
par liczb
całkowitych 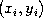 (
(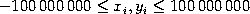 ), oznaczających współrzędne ko\-lejnych wierzchołków wielokąta
), oznaczających współrzędne ko\-lejnych wierzchołków wielokąta  (w kolejności zgodnej z kierunkiem ruchu wskazówek zegara). W trzeciej
i ostatniej linii wejścia znajduje się
(w kolejności zgodnej z kierunkiem ruchu wskazówek zegara). W trzeciej
i ostatniej linii wejścia znajduje się  par liczb całkowitych
par liczb całkowitych 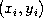 (
(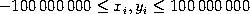 ) oznaczających
współrzędne kolejnych wierzchołków wielokąta
) oznaczających
współrzędne kolejnych wierzchołków wielokąta 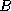 (w kolejności zgodnej z
kierunkiem ruchu wskazówek zegara).
(w kolejności zgodnej z
kierunkiem ruchu wskazówek zegara).
Wyjście
Pierwszy i jedyny wiersz powinien zawierać jedną liczbę całkowitą - podwojoną powierzchnię 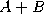 .
.
Przykład
Dla danych wejściowych:
4 4 0 0 0 1 2 1 2 0 0 0 0 2 1 2 1 0
poprawną odpowiedzią jest:
18
Autor zadania: Piotr Stańczyk.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English