
Zadanie Komiwojażer (sal)
Pomóż nam usprawnić bazę zadań!
Komiwojażer
Limit pamięci: 128 MB
Komiwojażer stwierdził, iż optymalne planowanie podróży na powierzchni ziemi
jest zbyt trudnym problemem obliczeniowym, więc przenosi swój interes w liniowy
świat na Dunaju.
Ów komiwojażer posiada bardzo szybką łódź, którą może przepłynąć pomiędzy dowolnymi
punktami na rzece w pomijalnym czasie, ale niestety łódź ta zużywa ogromne ilości paliwa --
każdy metr przepłynięty w górę rzeki (w kierunku jej źródła) kosztuje komiwojażera
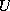 dolarów, a każdy metr przepłynięty w dół rzeki (w przeciwnym kierunku)
--
dolarów, a każdy metr przepłynięty w dół rzeki (w przeciwnym kierunku)
-- 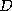 dolarów.
dolarów.
Wzdłuż rzeki jest rozmieszczonych 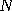 targów, które komiwojażer chciałby odwiedzić.
Każdy targ odbywa się tylko przez jeden dzień.
Dla każdego targu
targów, które komiwojażer chciałby odwiedzić.
Każdy targ odbywa się tylko przez jeden dzień.
Dla każdego targu 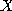 , komiwojażer zna jego datę
, komiwojażer zna jego datę 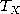 , wyrażoną jako liczba dni
od zakupu jego łodzi.
Zna też lokalizację targu
, wyrażoną jako liczba dni
od zakupu jego łodzi.
Zna też lokalizację targu 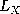 , będącą jego odległością w metrach od źródła rzeki
(w dół rzeki), jak również liczbę dolarów
, będącą jego odległością w metrach od źródła rzeki
(w dół rzeki), jak również liczbę dolarów 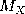 , którą zarobi, jeśli odwiedzi ten targ.
Powinien zacząć i zakończyć swoją podróż w swoim domu nad brzegiem rzeki, który
znajduje się na pozycji
, którą zarobi, jeśli odwiedzi ten targ.
Powinien zacząć i zakończyć swoją podróż w swoim domu nad brzegiem rzeki, który
znajduje się na pozycji 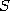 , także wyrażonej jako odległość w metrach od źródła rzeki.
, także wyrażonej jako odległość w metrach od źródła rzeki.
Pomóż komiwojażerowi wybrać targi, które powinien odwiedzić (potencjalnie żadne), oraz ich kolejność, tak aby zmaksymalizować zysk na końcu podróży. Zysk komiwojażera wyraża się jako suma dolarów uzyskanych na odwiedzonych targach minus suma dolarów wydanych na podróże w górę i w dół rzeki.
Pamiętaj, że jeśli targ 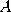 odbywa się przed targiem
odbywa się przed targiem 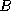 , komiwojażer może odwiedzić
je tylko w tej kolejności (tzn. nie może najpierw odwiedzić
, komiwojażer może odwiedzić
je tylko w tej kolejności (tzn. nie może najpierw odwiedzić 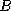 , a potem
, a potem 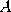 ).
Jeśli jednak dwa targi odbywają się tego samego dnia, komiwojażer może odwiedzić
je w dowolnej kolejności.
Nie ma ograniczenia na liczbę targów odwiedzonych jednego dnia, ale oczywiście
komiwojażer nie może odwiedzić dwa razy tego samego targu i zgarnąć zysków dwukrotnie.
Może natomiast przepłynąć obok odwiedzonych wcześniej targów bez dodatkowego zysku.
).
Jeśli jednak dwa targi odbywają się tego samego dnia, komiwojażer może odwiedzić
je w dowolnej kolejności.
Nie ma ograniczenia na liczbę targów odwiedzonych jednego dnia, ale oczywiście
komiwojażer nie może odwiedzić dwa razy tego samego targu i zgarnąć zysków dwukrotnie.
Może natomiast przepłynąć obok odwiedzonych wcześniej targów bez dodatkowego zysku.
Zadanie
Napisz program, który mając dane daty, lokalizacje i możliwe zyski z poszczególnych targów, jak również lokalizację domu komiwojażera i jego koszty podróżowania, wyznaczy maksymalny możliwy do uzyskania zysk na końcu podróży.
Ograniczenia
 -- liczba targów
-- liczba targów
 -- koszt podróżowania w górę rzeki (
-- koszt podróżowania w górę rzeki (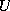 ) i w jej dół (
) i w jej dół (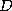 )
)
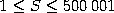 -- lokalizacja domu komiwojażera
-- lokalizacja domu komiwojażera
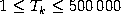 -- dzień, w którym odbywa się targ
-- dzień, w którym odbywa się targ 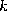
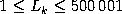 -- lokalizacja targu
-- lokalizacja targu 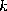
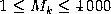 -- liczba dolarów, którą zarobi komiwojażer, jeśli odwiedzi targ
-- liczba dolarów, którą zarobi komiwojażer, jeśli odwiedzi targ 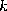
Wejście
Twój program powinien wczytać ze standardowego wejścia następujące dane:
- Pierwszy wiersz zawiera liczby całkowite
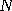 ,
, 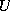 ,
, 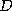 oraz
oraz 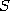 ,
w tej kolejności, pooddzielane pojedynczymi odstępami.
,
w tej kolejności, pooddzielane pojedynczymi odstępami.
- Kolejne
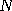 wierszy opisuje
wierszy opisuje 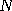 targów, w jakiejkolwiek kolejności.
targów, w jakiejkolwiek kolejności.
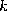 -ty z tych
-ty z tych 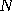 wierszy opisuje
wierszy opisuje 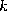 -ty targ i zawiera trzy liczby całkowite
pooddzielane pojedynczymi odstępami: dzień odbywania się targu
-ty targ i zawiera trzy liczby całkowite
pooddzielane pojedynczymi odstępami: dzień odbywania się targu 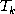 , jego
lokalizację
, jego
lokalizację 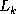 oraz zysk
oraz zysk 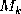 możliwy do uzyskania na nim przez komiwojażera.
możliwy do uzyskania na nim przez komiwojażera.
Uwaga: Wszystkie lokalizacje podane na wejściu będą różne. Dokładniej, żadne dwa targi nie będą odbywały się w tym samym miejscu i żaden targ nie odbędzie się w domu komiwojażera.
Wyjście
Twój program powinien wypisać na standardowe wyjście jeden wiersz zawierający jedną liczbę całkowitą: maksymalny zysk, jaki może uzyskać komiwojażer po odbyciu swej podróży.
Ocenianie
W testach wartych łącznie 60 punktów żadne dwa targi nie będą odbywać się tego samego dnia.
W testach wartych łącznie 40 punktów żadna z liczb na wejściu nie przekroczy 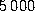 .
.
Testy, w których zachodzą oba powyższe warunki, są warte 15 punktów.
Testy, w których zachodzi co najmniej jeden z tych warunków, są warte 85 punktów.
Przykład
Dla danych wejściowych:
4 5 3 100 2 80 100 20 125 130 10 75 150 5 120 110
poprawną odpowiedzią jest:
50
Wyjaśnienie do przykładu: Optymalny plan podróży przewiduje odwiedzenie targów 1 i 3 (tych o lokalizacjach 80 i 75). Kolejność działań oraz odpowiadające im zyski i koszty są następujące:
- Komiwojażer podróżuje 20 metrów w górę rzeki kosztem 100 dolarów. Dotychczasowy zysk: -100.
- Odwiedza targ numer 1 i zyskuje 100. Dotychczasowy zysk: 0.
- Podróżuje 5 metrów w górę rzeki, ponosząc koszt 25. Dotychczasowy zysk: -25.
- Odwiedza targ numer 3, gdzie zarabia 150. Dotychczasowy zysk: 125.
- Podróżuje 25 metrów w dół rzeki i tym samym wraca do domu, ponosząc koszt 75. Zysk końcowy: 50.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English