Game

Memory limit: 8 MB

Two players, 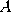and 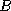, play a game on a square board of size 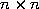. The squares of the board are either white or black. The game is played only on the white squares - the black ones are excluded from the game. Each player has one piece, initially placed at this player's starting point - one of the white squares on the board. The starting point of 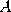is different than that of .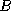

In each move a player moves his piece to one of the neighboring white squares (either up, down, left or right). If the player moves his piece to the square currently occupied by his opponent's piece, he gets an extra move (this way he jumps over the opponent). Note that in this case the direction of the second move can be different than that of the first move.

Player 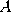moves first, then players alternate. The goal of the game is to reach the opponent's starting point. The player whose piece reaches his opponent's starting point first, wins the game. Even if the player's last move consists of two jumps, and he only jumps over his opponent's starting point (since it is occupied by his opponent), the player wins. We want to determine which player has a winning strategy (a player has a winning strategy if he can win regardless of his opponent's moves).

Figure 1. If 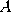moves to the right on his first three moves, 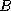will move up the first three moves. Thus, on the third move player 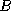will reach the square with 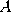's piece and will be allowed to move again. Because of this, 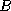will reach 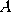's starting point first and will win the game.

Figure 2. 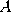can start by moving one step to the right and one step down. Then, depending on the first two moves of 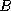, he will either go down or right and evade 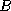. This way 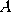will reach 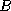's starting point first, thus winning the game. In fact we proved that 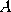has a winning strategy.

Task

Write a program, that:

• reads the layout of the grid and the starting points of the two players from the standard input,
• finds the player who has a winning strategy,
• writes the result to the standard output.

Input

The first line of the standard input contains one integer 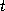the number of test cases (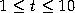). After it the description of 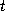tests appears. Each test is described as follows. In the first line of the test there is one integer (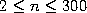), the length of the side of the grid. Then next lines contain the description of the grid. Each line consists of characters (with no white-spaces between them). Each character is either '.' (a white square), '#' (a black square), 'A' (the starting point of 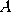) or 'B' (the starting point of ).

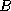You may assume that there exists a path of white squares between the starting points of 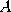and .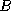

Additionally, in test cases worth 60% of poin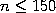ts, and in test cases worth 40% of points, .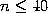

Output

For each test case exactly one line should be printed to standard output containing a single character 'A' or 'B', indicating the player who has a winning strategy.

Example

For the input data:

2
4
A...
.#..
....
...B
4
A...
....
..#.
...B

the correct result is:

B
A

Task author: Jimmy Mårdell.