Rods

Memory limit: 32 MB

In laboratories of a certain company a new material called politoksyparen is tested. During the researches an interesting property has been discovered. A simple rod made of this material after being heated lengthens and bends so that it changes into an circular arc based on a chord, which is the shape of the rod at the beginning (this property concerns only rods of short diameters). Let's assume that rods with very short diameters and lengths 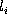(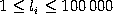) were used to verify this property, and while being heated they lengthened respectively by 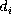(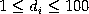), where 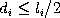. As a unit we take one millimeter.

Task

Write a program that:

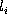• reads from the standard input a number of rods , their lengths and increases in lengths ,
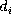• computes for each rod a distance between the middle of the chord and the middle of the arc after heating (assuming that politoksyparen has indeed the observed property, and rods really band into circular arcs while being heated); the result should be an integer which differs no more then 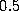from the exact result,
• writes the solution to the standard output.

Input

In the first line of the standard input there is written one positive integer (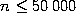). In each of the following lines there are written two integers separated by a single space — the original length of the rod 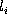and its increase in length during heating .

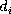Output

In each of lines of the standard output there should be written one nonnegative integer. The integer in 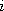-th line should be equal to the distance between the positions of the middle of the 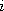-th rod before and after heating computed with a required accuracy.

Example

For the input data:

2
1000 20
15000 10

the correct result is:

87
237

Task author: Piotr Chrzastowski-Wachtel.