
Zadanie Pytania (A) (pyt)
Pomóż nam usprawnić bazę zadań!
Pytania [A]
Limit pamięci: 32 MB
Pewnego razu król Bajtur wymyślił grę dla swoich synów. Opowiedział on o niej swojemu doradcy, magowi Bajtlinowi, w następujący sposób:
Ustawiłem trzech moich synów (ponumerowanych liczbami 1, 2, 3) w szereg, a następnie każdemu z nich włożyłem na głowę złotą albo srebrną koronę. Syn numer 1 widział korony na głowach synów 2 i 3, a syn numer 2 widział koronę na głowie 3. Każdy z synów wiedział, że w sumie są co najwyżej dwie złote korony. Następnie spytałem syna numer 1, czy wie, jakiego koloru ma koronę. Odpowiedział on, że nie wie. Potem spytałem syna numer 2, czy wie, jakiego koloru ma koronę. Odpowiedział, że również nie wie.
W tym momencie Bajtlin przerwał Bajturowi i powiedział, że on już wie, jaką koronę dostał królewicz 3. Bajtur go się spytał, skąd to wie. Odpowiedział on następująco:
Gdyby królewicz 1 widział dwie złote korony, to wiedziałby, że sam ma srebrną (gdyż są co najwyżej dwie złote). Skoro odpowiedział NIE, znaczy to, że tak nie jest. Teraz gdyby królewicz 2 widział złotą koronę na głowie królewicza 3, to wiedziałby, że sam ma srebrną - inaczej królewicz 1 odpowiedziałby TAK. Jednak tego nie wiedział. Zatem królewicz 3 musi mieć srebrną koronę.
Twoim zadaniem jest napisanie (w miarę) ogólnego symulatora powyższego rodzaju sytuacji. Fakty, o które król może pytać królewiczów albo maga (w powyższej sytuacji był to rodzaj korony), są zakodowane jako ciąg zmiennych. Część z nich jest w określonej relacji z poprzednimi zmiennymi, a o reszcie wiadomo jedynie, z jakiego są zakresu. Dokładniejszy opis zagadnienia do rozwiązania znajduje się w sekcji Wejście.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia opis sytuacji,
- wyznaczy odpowiedzi, jakich powinien udzielić mag,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu wejścia podane są trzy liczby całkowite 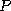 ,
, 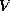 oraz
oraz 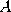 , pooddzielane pojedynczymi odstępami.
, pooddzielane pojedynczymi odstępami.
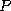 określa liczbę królewiczów (ponumerowanych od
określa liczbę królewiczów (ponumerowanych od 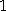 do
do 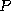 ),
), 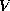 - liczbę zmiennych (ponumerowanych od
- liczbę zmiennych (ponumerowanych od 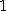 do
do 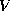 ),
),
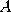 - liczbę akcji. Możesz założyć, że spełnione są następujące nierówności:
- liczbę akcji. Możesz założyć, że spełnione są następujące nierówności: 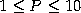 ,
, 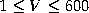 ,
, 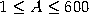 .
.
Kolejne
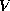 wierszy określa kolejne zmienne
wierszy określa kolejne zmienne 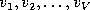 . Każdy z tych
wierszy jest postaci "
. Każdy z tych
wierszy jest postaci "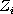
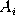
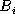 " (w zapisie występują pojedyncze odstępy),
gdzie
" (w zapisie występują pojedyncze odstępy),
gdzie 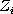 jest jednym ze znaków
jest jednym ze znaków  ,
,  ,
,  ,
,  ,
, 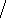 ,
, 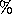 ,
, 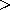 , zaś
, zaś 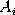 oraz
oraz 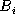 są liczbami całkowitymi.
W zależności od
są liczbami całkowitymi.
W zależności od 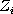 występującego w opisie
występującego w opisie 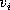 , otrzymujemy różnego rodzaju
informacje na temat tej zmiennej. Znaczenie poszczególnych znaków jest opisane poniżej:
, otrzymujemy różnego rodzaju
informacje na temat tej zmiennej. Znaczenie poszczególnych znaków jest opisane poniżej:
= 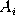 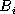 |
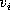 jest liczbą całkowitą między jest liczbą całkowitą między 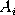 a a 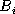 (zachodzi wówczas nierówność (zachodzi wówczas nierówność 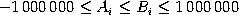 ) ) |
+ 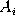 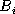 |
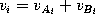 (w tym i każdym następnym przypadku zachodzi (w tym i każdym następnym przypadku zachodzi 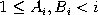 ) ) |
- 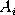 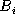 |
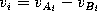 |
*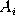 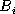 |
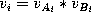 |
/ 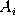 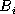 |
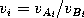 (część całkowita) (część całkowita) |
% 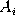 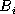 |
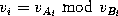 (reszta z dzielenia) (reszta z dzielenia) |
> 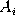 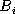 |
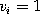 jeśli jeśli 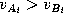 ; ; 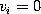 w przeciwnym przypadku w przeciwnym przypadku |
Ta informacja jest dostępna na początku gry wszystkim królewiczom, a także magowi.
W kolejnych 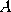 wierszach podane są akcje. Akcje mogą być następujących rodzajów
(w zapisach akcji występują pojedyncze odstępy):
wierszach podane są akcje. Akcje mogą być następujących rodzajów
(w zapisach akcji występują pojedyncze odstępy):
- S
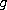

Wartość
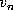 została ujawniona synowi numer
została ujawniona synowi numer 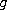 .
O fakcie ujawnienia tej wartości synowi dowiedzieli się wszyscy królewicze, a także mag
(co nie oznacza, że poznali oni samą tę wartość).
.
O fakcie ujawnienia tej wartości synowi dowiedzieli się wszyscy królewicze, a także mag
(co nie oznacza, że poznali oni samą tę wartość).
- T
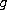

Król spytał syna o numerze
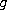 , czy zna wartość
, czy zna wartość 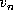 . Dostał odpowiedź
TAK, którą przekazał magowi (Pozostali synowie usłyszą odpowiedź dopiero wtedy,
kiedy wykonana zostanie akcja A - dzięki temu kilku z nich może "jednocześnie"
odpowiadać na pytania, i odpowiedzi jednych nie będą od razu wykorzystywane
przez drugich).
. Dostał odpowiedź
TAK, którą przekazał magowi (Pozostali synowie usłyszą odpowiedź dopiero wtedy,
kiedy wykonana zostanie akcja A - dzięki temu kilku z nich może "jednocześnie"
odpowiadać na pytania, i odpowiedzi jednych nie będą od razu wykorzystywane
przez drugich).
- N

Jak wyżej, tylko król uzyskał odpowiedź NIE.
- X

Jak wyżej, tylko król nie przekazał magowi, jaka była odpowiedź, ale kazał magowi zgadywać. Mag odpowiada królowi TAK, NIE albo NIE WIEM (odpowiedź NIE WIEM oznacza, że mag nie jest pewien, czy syn znał odpowiedź na pytanie króla, czy nie). Król przy okazji tej akcji nie informuje maga, jaka była faktyczna odpowiedź królewicza
 .
Król również nie informuje królewiczów, co odpowiedział mag.
.
Król również nie informuje królewiczów, co odpowiedział mag.
- A
Wszystkim synom zostają przekazane dotychczasowe odpowiedzi pozostałych synów na wszystkie pytania króla (odpowiedzi, które padały przy okazji akcji typu T, N oraz X). Król tutaj również nie informuje maga, jakie odpowiedzi uzyskał na pytania w akcjach typu X.
- M

Król powiedział magowi, że zmienna
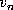 ma wartość
ma wartość 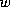 .
.
- Q
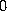

Król pyta się maga, jakie są - zgodnie z jego aktualną wiedzą - możliwe wartości
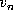 .
Król nie informuje królewiczów, co odpowiedział mag.
.
Król nie informuje królewiczów, co odpowiedział mag.
Należy założyć, że zarówno królewicze, jak i mag, wnioskują w doskonały sposób, to znaczy są w stanie w każdym momencie wydedukować wszystkie informacje, które wynikają z ograniczeń ujawnionych przez króla na początku gry oraz z jej dotychczasowego przebiegu. Co więcej, każdy z nich wie, że wszyscy wnioskują w doskonały sposób.
Ograniczenia:
Są spełnione następujące ograniczenia: 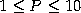 ,
,
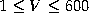 ,
, 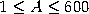 . Dodatkowo liczba wszystkich
możliwości (czyli iloczyn wartości
. Dodatkowo liczba wszystkich
możliwości (czyli iloczyn wartości 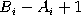 po wszystkich zmiennych typu "
po wszystkich zmiennych typu " ")
nie przekracza
")
nie przekracza 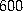 .
W każdym teoretycznie możliwym na początku gry przypisaniu wartości zmiennym,
bezwzględna wartość żadnej zmiennej
nie przekracza
.
W każdym teoretycznie możliwym na początku gry przypisaniu wartości zmiennym,
bezwzględna wartość żadnej zmiennej
nie przekracza 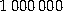 , a w przypadku operacji "
, a w przypadku operacji "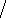 " i "
" i "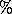 "
"
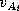 jest nieujemne, a
jest nieujemne, a 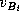 jest dodatnie.
Zmienna
jest dodatnie.
Zmienna 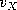 może występować w definicji
może występować w definicji 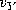 tylko dla
tylko dla 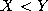 .
.
Wyjście
Dla każdej akcji typu Q należy wypisać jeden wiersz, zawierający ciąg możliwych wartości 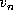 ,
od najmniejszej do największej, pooddzielanych pojedynczymi odstępami.
Dla każdej akcji typu X należy wypisać jeden wiersz zawierający TAK, NIE albo NIE WIEM.
Odpowiedzi na wyjściu należy wypisać w kolejności zgodnej z kolejnością akcji (na wejściu), których dotyczą,
czyli niezależnie od typów tych akcji.
,
od najmniejszej do największej, pooddzielanych pojedynczymi odstępami.
Dla każdej akcji typu X należy wypisać jeden wiersz zawierający TAK, NIE albo NIE WIEM.
Odpowiedzi na wyjściu należy wypisać w kolejności zgodnej z kolejnością akcji (na wejściu), których dotyczą,
czyli niezależnie od typów tych akcji.
Przykład
Dla danych wejściowych:
| 3 7 16 | 3 królewicze, 7 zmiennych, 16 akcji |
| = 0 1 | 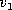 : kolor korony syna 1 (0 = srebrna, 1 = złota) : kolor korony syna 1 (0 = srebrna, 1 = złota) |
| = 0 1 | 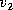 : kolor korony syna 2 : kolor korony syna 2 |
| = 0 1 | 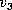 : kolor korony syna 3 : kolor korony syna 3 |
| + 1 2 | 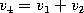 |
| + 3 4 | 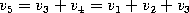 , czyli innymi słowy łączna liczba złotych koron , czyli innymi słowy łączna liczba złotych koron |
| = 3 3 | 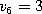 |
| > 6 5 | 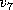 określa, czy złotych koron jest mniej niż 3 określa, czy złotych koron jest mniej niż 3 |
| S 1 7 | Wszyscy synowie wiedzą, że są mniej niż 3 złote korony. |
| S 2 7 | |
| S 3 7 | |
| M 1 7 | Mag też to wie. |
| S 1 3 | Królewicz 1 widzi koronę królewicza 3. |
| S 2 3 | Królewicz 2 widzi koronę królewicza 3. |
| S 1 2 | Królewicz 1 widzi koronę królewicza 2. |
| X 3 3 | Czy (według maga) syn 3 wie, jaką ma koronę? (nie) |
| X 1 1 | Czy (według maga) syn 1 wie, jaką ma koronę? (mag nie wie) |
| N 1 1 | Syn 1 nie zna koloru swojej korony. |
| A 0 0 | Wszyscy synowie się dowiadują, że 1 i 3 nie znają kolorów swoich koron. |
| N 2 2 | Syn 2 odpowiada, że nadal nie zna koloru swojej korony. |
| X 3 3 | Mag wie, że syn 3 nadal nie wie, jaką ma koronę (nie słyszy odpowiedzi 2). |
| A 0 0 | |
| X 3 3 | Teraz syn 3 już wie. |
| Q 0 3 | Mag też wie, że królewicz 3 ma koronę typu 0. |
poprawną odpowiedzią jest:
NIE NIE WIEM NIE TAK 0
Autor zadania: Eryk Kopczyński.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English