Addon

Memory limit: 32 MB

Scientists discovered a new radioactive element — addon. It appeared that addon was the most efficient nuclear fuel ever known so it was decided that an addon reactor should be constructed. According to the project a fuel chamber is a vertical pipe. Fuel rods, i.e. addon cylinders, are placed in a chamber one above another. Fuel rods have various lengths.

The cycle of the reactor begins with putting fuel rods into the chamber. The next step is the ignition. Unfortunately, the height of a column of fuel cannot be arbitrary — only certain heights ensure safety of the reaction. Such heights are called stable heights.

Designers of a reactor have two tasks: to establish the height of the fuel chamber and to chose the set of lengths, in which addon rods will be produced. We say that a set of lengths is safe (for a given chamber) if for any column, which is constructed from rods whose lengths belong to this set and which is not higher than the height of the chamber, the height of this column is stable. We say that a set of lengths is complete (for a given chamber) if every column of stable height, not higher than the height of the chamber, can be constructed of rods, whose lengths are taken from this set.

Task

Write a program that:

• reads the set of stable heights from the standard input,
• computes the maximal height of a chamber for which a safe and complete set of lengths exists,
• finds for such a chamber a safe and complete set of lengths with minimal possible number of elements,
• writes the result to the standard output.

Input

In the first line of the standard input there is a natural number , , 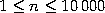which is the number of given stable heights. In each of the following lines there is one positive integer, not greater than 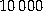. These numbers represent stable heights and are given in increasing order.

Output

In the first line of the standard output there should be written one integer — the maximal height of a chamber. In the following lines there should be written (in increasing order) computed set of lengths (one number in one line).

Example

For the input data:

14
5
10
12
15
17
20
21
22
24
26
27
30
31
33

the correct result is:

24
5
12
21

Task author: Grzegorz Jakacki.