
Zadanie Gdzie zbudować browar? (bro)
Pomóż nam usprawnić bazę zadań!
Gdzie zbudować browar?
Limit pamięci: 32 MB
Mieszkańcy bajtockiej wyspy Abstynencja bardzo lubią piwo bezalkoholowe. Do tej pory piwo bezalkoholowe sprowadzano z Polski, ale w tym roku w jednym z miast na Abstynencji zostanie wybudowany browar. Wszystkie miasta wyspy leżą na wybrzeżu i są połączone autostradą obiegającą wyspę wzdłuż brzegu. Inwestor budujący browar zebrał informacje o zapotrzebowaniu na piwo, tj. ile cystern piwa trzeba codziennie dostarczyć do każdego z miast. Dysponuje także zestawieniem odległości pomiędzy miastami. Koszt transportu jednej cysterny na odległość 1 km wynosi 1 talar. Dzienny koszt transportu to suma, jaką trzeba wyłożyć, by do każdego miasta przetransportować z browaru tyle cystern, ile wynosi zapotrzebowanie w danym mieście. Jego wielkość zależy od miejsca położenia browaru. Inwestor chce zminimalizować koszty transportu piwa.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia liczbę miast, odległości między nimi oraz dzienne zapotrzebowania na piwo,
- obliczy minimalny dzienny koszt transportu piwa,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia jest zapisana jedna liczba
całkowita  równa liczbie miast,
równa liczbie miast, 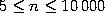 . W każdym z kolejnych
. W każdym z kolejnych
 wierszy zapisana jest para nieujemnych liczb całkowitych oddzielonych
pojedynczym odstępem.
Liczby
wierszy zapisana jest para nieujemnych liczb całkowitych oddzielonych
pojedynczym odstępem.
Liczby 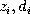 zapisane w
zapisane w 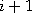 -ym wierszu to odpowiednio
zapotrzebowanie na piwo w mieście nr
-ym wierszu to odpowiednio
zapotrzebowanie na piwo w mieście nr 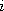 oraz odległość (w kilometrach)
od miasta nr
oraz odległość (w kilometrach)
od miasta nr 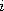 do następnego miasta na autostradzie. Kolejne miasta na
autostradzie mają kolejne numery, po mieście nr
do następnego miasta na autostradzie. Kolejne miasta na
autostradzie mają kolejne numery, po mieście nr  leży miasto nr 1.
Całkowita długość autostrady nie przekracza
leży miasto nr 1.
Całkowita długość autostrady nie przekracza 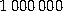 km.
Zapotrzebowanie na piwo w żadnym mieście nie przekracza
km.
Zapotrzebowanie na piwo w żadnym mieście nie przekracza 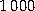 cystern.
cystern.
Wyjście
Twój program powinien zapisać w pierwszym i jedynym wierszu standardowego wyjścia dokładnie jedną liczbę całkowitą równą minimalnemu dziennemu kosztowi transportu piwa.
Przykład
Dla danych wejściowych:
6 1 2 2 3 1 2 5 2 1 10 2 3
poprawną odpowiedzią jest:
41
Autor zadania: Wojciech Guzicki.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English