
Zadanie Podzbiory [A] (pod)
Pomóż nam usprawnić bazę zadań!
Subsets [A]
Memory limit: 32 MB
We are going to consider subsets 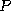 of a given set
of a given set 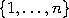 .
We are interested in subsets such that for a given natural number
.
We are interested in subsets such that for a given natural number 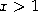 and for
any natural number
and for
any natural number 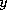 at least one of the numbers
at least one of the numbers 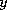 ,
, 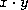 doesn't belong to
doesn't belong to 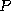 .
We would like to calculate the number of such subsets, that have exactly
.
We would like to calculate the number of such subsets, that have exactly 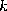 elements.
It is possible that the number of such subsets is huge - therefore it is sufficient to calculate the remainder of the division
of the result by
elements.
It is possible that the number of such subsets is huge - therefore it is sufficient to calculate the remainder of the division
of the result by 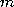 .
.
Task
Write a program which:
- reads from the standard input four integers:
 ,
, 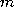 ,
, 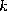 and
and  ,
,
- calculates the remainder of the division by
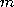 of the number of
of the number of 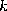 -element subsets of set
-element subsets of set 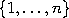 , that fulfill
the requirements described above,
, that fulfill
the requirements described above,
- writes result to the standard output.
Input
In the first and only line of the standard input there are four integers  ,
, 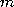 ,
, 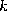 and
and  (
(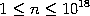 ,
,
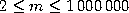 ,
, 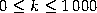 ,
,
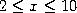 ), separated by single spaces.
), separated by single spaces.
Output
The first and only line should contain one integer - the reminder of the division by 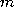 of the number of
of the number of 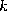 -element subsets
of set
-element subsets
of set 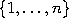 that fulfill the specified requirements.
that fulfill the specified requirements.
Example
For the input data:
6 1234 3 2
the correct result is:
9
Considered subsets are:
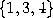 ,
,
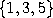 ,
,
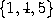 ,
,
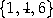 ,
,
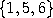 ,
,
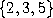 ,
,
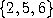 ,
,
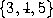 and
and
 .
.
Task author: Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English