
Zadanie Ryby [A] (ryb)
Pomóż nam usprawnić bazę zadań!
Ryby [A]
Limit pamięci: 256 MB
W wodach pewnego archipelagu żyje rzadki gatunek drapieżnych ryb. Prowadzą one bardzo regularny tryb życia. Każda ryba budzi się codziennie o tej samej porze i wypływa na polowanie. Wieczorem, po zakończonych łowach, wraca w miejsce, z którego wyruszyła. Tam kładzie się spać (każdego dnia o tej samej godzinie), jednak może obudzić się następnego dnia w innym miejscu, gdyż prądy morskie mogą ją nieco znieść.
W ciągu całego dnia ryba zachowuje następującą zasadę: w każdym momencie musi widzieć punkt, w którym była w tym samym momencie poprzedniego dnia, czyli dokładnie 24 godziny wcześniej. Oczywiście, ryba nie może widzieć punktu, który jest po przeciwnej stronie jakiejś wyspy.
Ichtiolodzy przez dłuższy czas prowadzili obserwację ryb w archipelagu i co kilka dni notowali jedną trasę, którą w ciągu tego dnia przepłynęła pewna ryba. Niestety po zgromadzeniu dużej ilości danych nastąpił wypadek, i dokumentacja rozsypała się przy przenoszeniu. Część informacji całkowicie zaginęła, a reszta jest pomieszana. Ichtiolodzy nie wiedzą nawet, która trasa opisuje ruch której z ryb. Proszą Cię zatem o pomoc - przekażą Ci pomieszany zbiór opisów tras, a Ty im powiesz, jaka mogła być minimalna liczba różnych ryb, które obserwowali podczas badań.
Wejście
Twój program powinien czytać dane ze standardowego wejścia.
Wejście składa się z dwóch części: z opisu archipelagu i opisu tras ryb.
Pierwszy wiersz opisu archipelagu zawiera dwie liczby całkowite
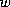 oraz
oraz 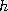 (
(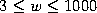 ,
, 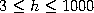 ), oddzielone
pojedynczym odstępem.
W każdym z kolejnych
), oddzielone
pojedynczym odstępem.
W każdym z kolejnych 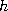 wierszy znajduje się opis fragmentu archipelagu w postaci
ciągu
wierszy znajduje się opis fragmentu archipelagu w postaci
ciągu 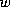 znaków.
Znak '.' oznacza ocean, a '#' - ląd.
We wszystkich polach na brzegu mapy jest woda (znak '.').
znaków.
Znak '.' oznacza ocean, a '#' - ląd.
We wszystkich polach na brzegu mapy jest woda (znak '.').
Z pewnego punktu w oceanie ryba widzi inny, jeśli odcinek, który je łączy, nie ma punktów wspólnych z wnętrzem ani brzegiem jakiegokolwiek fragmentu lądu. Kierunek płynięcia ryby nie ma tu znaczenia.
W następnym wierszu znajduje się liczba całkowita  (
(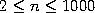 ), oznaczająca
liczbę zanotowanych tras ryb.
W kolejnych
), oznaczająca
liczbę zanotowanych tras ryb.
W kolejnych 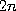 wierszach następują opisy poszczególnych tras.
W pierwszym wierszu opisu trasy znajdują się trzy liczby całkowite
wierszach następują opisy poszczególnych tras.
W pierwszym wierszu opisu trasy znajdują się trzy liczby całkowite  ,
, 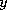 oraz
oraz  (
(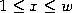 ,
, 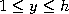 ,
,  ), pooddzielane pojedynczymi odstępami.
Liczby
), pooddzielane pojedynczymi odstępami.
Liczby  i
i 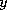 to współrzędne miejsca, w którym ryba się obudziła (numer kolumny i wiersza mapy), zaś
to współrzędne miejsca, w którym ryba się obudziła (numer kolumny i wiersza mapy), zaś  to
długość trasy.
Drugi wiersz składa się z
to
długość trasy.
Drugi wiersz składa się z  znaków N, W, S lub E
określających kierunek płynięcia ryby.
Oznaczają one odpowiednio kierunki: w górę, w lewo, w dół i w prawo.
Opis trasy jest tak skonstruowany, że przebiega ona jedynie po polach z wodą,
nie wybiega poza fragment archipelagu opisany w wejściu, a jej koniec wypada w tym samym miejscu co początek.
znaków N, W, S lub E
określających kierunek płynięcia ryby.
Oznaczają one odpowiednio kierunki: w górę, w lewo, w dół i w prawo.
Opis trasy jest tak skonstruowany, że przebiega ona jedynie po polach z wodą,
nie wybiega poza fragment archipelagu opisany w wejściu, a jej koniec wypada w tym samym miejscu co początek.
Ryba porusza się jedynie w pionie lub poziomie i podczas polowania płynie po łamanej łączącej środki pól na ścieżce; nie znamy jednak jej prędkości. Prędkość ta nie musiała być stała na całej trasie, ryba mogła przyspieszać i zwalniać, byleby tylko widzieć punkt, w którym była dokładnie dobę wcześniej.
Prądy morskie mogą znieść śpiącą rybę co najwyżej o jedno pole w górę, dół, lewo lub prawo od miejsca, w którym położyła się ona spać. Możesz założyć, że dla dowolnych dwóch pól oznaczających wodę, istnieje (hipotetyczna) trasa ryby, która przez nie przepływa.
Wyjście
W pierwszym wierszu standardowego wyjścia należy wypisać liczbę całkowitą 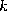 - najmniejszą możliwą liczbę różnych ryb, jaka pasuje do danych zebranych
przez ichtiologów.
W każdym z kolejnych
- najmniejszą możliwą liczbę różnych ryb, jaka pasuje do danych zebranych
przez ichtiologów.
W każdym z kolejnych 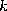 wierszy powinny znaleźć się listy numerów tras, które
mogła pokonać dana ryba - trasy nie musiały jednak zostać przez nią
przebyte w kolejnych dniach, a potencjalnie w dowolnych momentach
jej życia.
wierszy powinny znaleźć się listy numerów tras, które
mogła pokonać dana ryba - trasy nie musiały jednak zostać przez nią
przebyte w kolejnych dniach, a potencjalnie w dowolnych momentach
jej życia.
Dwie trasy mogą być pokonane przez daną rybę w dwóch kolejnych dniach, jeżeli zaczynają się w tym samym bądź w sąsiednich (mających wspólną krawędź) polach oraz jeżeli ryba mogła przepłynąć je tak, żeby w każdym momencie dnia, płynąc po drugiej trasie, widziała punkt z pierwszej trasy, w którym była dokładnie dobę wcześniej.
Trasy są ponumerowane od 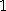 do
do  , zgodnie z kolejnością w wejściu.
Numery tras w każdym wierszu wyjścia należy wypisać w kolejności rosnącej,
natomiast wiersze muszą być wypisane w takiej kolejności, by pierwsze numery
w każdym z nich tworzyły ciąg rosnący.
, zgodnie z kolejnością w wejściu.
Numery tras w każdym wierszu wyjścia należy wypisać w kolejności rosnącej,
natomiast wiersze muszą być wypisane w takiej kolejności, by pierwsze numery
w każdym z nich tworzyły ciąg rosnący.
Przykład
Dla danych wejściowych:
10 8 .......... .......#.. ........#. .......... ...#...... ......###. ......###. .......... 4 2 7 12 NNNEEESSSWWW 2 8 24 WNNNNNNNEEEEESSSSSSSWWWW 1 8 46 NNNNNNNEEEEESSSSSSSEEEENNNNNNNSSSSSSSWWWWWWWWW 1 8 32 NNNNNNNEEEEEEEEESSSSSSSWWWWWWWWW
poprawną odpowiedzią jest:
2 1 2 3 4
Wyjaśnienie do przykładu. Pierwsze dwie trasy mogły być przebyte przez tę samą rybę (nawet w dwóch kolejnych dniach). Po kilku kolejnych dniach ryba mogła popłynąć trzecią trasą. Ostatnia trasa musiała być jednak przebyta przez inną rybę. W przeciwieństwie do pierwszych trzech, okrąża ona dużą wyspę.
Autor zadania: Eryk Kopczyński.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English