Termites [A]

Memory limit: 256 MB

Two termites are eating an old wooden fence. This fence consists of planks of possibly different heights. Termites have already eaten some of them, and they thought that they should make their meal more interesting. They have decided to play a game and eat the planks in turns, one by one. During one turn, a termite may choose to eat only a plank which is next to a plank that has already been consumed.

Assuming that each termite chooses the planks in such a way, that during the whole game the sum of heights of all planks eaten by her is as big as possible, compute the amount of wood that each of them will have eaten.

Input

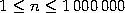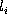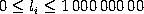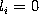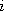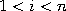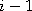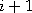In the first line of the standard input there is an integer (), denoting the number of planks in the fence. The second line contains a sequence of integers (), that describe the heights of the consecutive planks. If , then the corresponding plank has already been eaten. The plank number (for ) is next to the planks number and . The only plank adjacent to the plank number 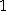is the plank number 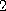, and the only plank next to the plank number is the plank number 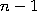. 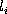At least one of 's is equal to zero.

Output

You should write two integers to the first and only line of the standard output. The first integer should be the sum of the heights of the planks that will be consumed by the termite which starts the game, whereas the second one should be equal to the amount of wood that will go to his opponent.

Example

For the input data:

8
1 2 0 3 7 4 0 9

the correct result is:

17 9

Explanation of the example: The fence consisted of 8 planks, out of which 2 have already been eaten. The first termite in his first turn can choose between planks of heights 2, 3, 4 and 9. During the optimal game, in the consecutive turns, termites will eat planks of heights 9, 2, 1, 4, 7 and 3.

Task author: Tomasz Idziaszek.