
Zadanie Estetyczny tekst (est)
Pomóż nam usprawnić bazę zadań!
Estetyczny tekst
Limit pamięci: 128 MB
Rozważmy dowolny tekst złożony z  słów ponumerowanych od
słów ponumerowanych od 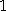 do
do  .
Dowolny podział tego tekstu na
.
Dowolny podział tego tekstu na 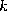 wierszy reprezentujemy za
pomocą takiego ciągu liczb
wierszy reprezentujemy za
pomocą takiego ciągu liczb 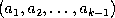 , że słowa
o numerach od
, że słowa
o numerach od 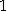 do
do 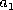 znajdują się w pierwszym wierszu,
słowa o numerach od
znajdują się w pierwszym wierszu,
słowa o numerach od 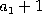 do
do 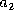 znajdują się w drugim wierszu
itd., a słowa o numerach od
znajdują się w drugim wierszu
itd., a słowa o numerach od 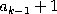 do
do  znajdują się
w ostatnim,
znajdują się
w ostatnim, 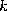 -tym wierszu.
-tym wierszu.
Każde słowo ma określoną długość (wyrażoną liczbą znaków).
Długość słowa o numerze  oznaczamy przez
oznaczamy przez
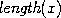 .
Ponadto każde dwa sąsiednie słowa w wierszu są oddzielone
odstępem szerokości jednego znaku.
Długością wiersza nazywamy sumę długości wszystkich słów w tym wierszu
powiększoną o liczbę odstępów między nimi.
Długość wiersza o numerze
.
Ponadto każde dwa sąsiednie słowa w wierszu są oddzielone
odstępem szerokości jednego znaku.
Długością wiersza nazywamy sumę długości wszystkich słów w tym wierszu
powiększoną o liczbę odstępów między nimi.
Długość wiersza o numerze 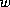 oznaczamy przez
oznaczamy przez 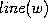 .
Oznacza to, że jeżeli w wierszu o numerze
.
Oznacza to, że jeżeli w wierszu o numerze 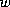 znajdują się słowa o numerach
od
znajdują się słowa o numerach
od 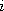 do
do 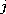 włącznie, to długość tego wiersza wynosi:
włącznie, to długość tego wiersza wynosi:
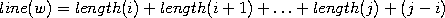
Dla przykładu, rozważmy tekst złożony z  słów o długościach
kolejno
słów o długościach
kolejno  ,
, 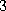 ,
, 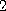 i
i 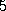 oraz jego podział
oraz jego podział 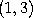 na
na 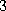 wiersze.
Wówczas długość pierwszego wiersza wynosi
wiersze.
Wówczas długość pierwszego wiersza wynosi  , drugiego -
, drugiego - 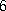 ,
a trzeciego -
,
a trzeciego - 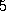 :
:
XXX XX (2. wiersz)
XXXXX (3. wiersz)
Współczynnikiem estetyczności podziału danego tekstu na 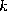 wierszy nazywamy liczbę wyrażoną wzorem:
wierszy nazywamy liczbę wyrażoną wzorem:
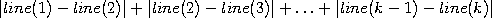
W szczególności, jeżeli podział zajmuje tylko jeden wiersz,
jego współczynnik estetyczności jest równy 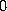 .
.
Im mniejszy jest współczynnik estetyczności, tym bardziej
estetyczny jest dany podział.
Rozpatrujemy tylko takie podziały, w których długość żadnego wiersza nie
przekracza pewnej stałej liczby 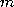 .
Spośród wszystkich takich podziałów danego tekstu na dowolną
liczbę wierszy poszukujemy podziału najbardziej estetycznego,
czyli o minimalnym współczynniku estetyczności.
W podanym powyżej przykładzie współczynnik estetyczności podziału
jest równy
.
Spośród wszystkich takich podziałów danego tekstu na dowolną
liczbę wierszy poszukujemy podziału najbardziej estetycznego,
czyli o minimalnym współczynniku estetyczności.
W podanym powyżej przykładzie współczynnik estetyczności podziału
jest równy 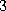 i jest to minimalna wartość współczynnika estetyczności dla
i jest to minimalna wartość współczynnika estetyczności dla
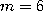 lub
lub 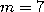 .
.
Zadanie
Napisz program, który:
-
wczyta ze standardowego wejścia liczby
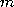 i
i  oraz
długości kolejnych słów,
oraz
długości kolejnych słów,
-
wyznaczy minimalny współczynnik estetyczności dla tych
podziałów, w których długość żadnego wiersza nie przekracza
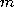 ,
,
- wypisze wynik na standardowe wyjście.
Wejście
Pierwszy wiersz standardowego wejścia zawiera liczby całkowite
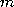 i
i  ,
, 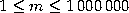 ,
, 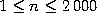 ,
oddzielone pojedynczym odstępem.
Drugi i ostatni wiersz wejścia zawiera
,
oddzielone pojedynczym odstępem.
Drugi i ostatni wiersz wejścia zawiera  liczb całkowitych będących
długościami kolejnych słów,
liczb całkowitych będących
długościami kolejnych słów, 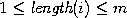 dla
dla
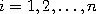 , pooddzielanych pojedynczymi odstępami.
, pooddzielanych pojedynczymi odstępami.
Wyjście
Pierwszy i jedyny wiersz standardowego wyjścia powinien zawierać
jedną liczbę całkowitą:
minimalny współczynnik estetyczności dla tych podziałów,
w których długość żadnego wiersza nie przekracza 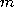 .
.
Przykład
Dla danych wejściowych:
6 4 4 3 2 5
poprawnym wynikiem jest:
3
a dla danych wejściowych:
4 2 1 2
poprawnym wynikiem jest:
0
Autor zadania: Bartosz Walczak.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English