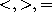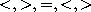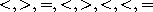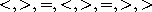Zadanie Monotoniczność (mon)
Pomóż nam usprawnić bazę zadań!
Monotoniczność
Limit pamięci: 256 MB
Schematem monotoniczności ciągu liczb całkowitych 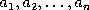 nazwiemy ciąg
nazwiemy ciąg 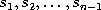 złożony ze znaków
złożony ze znaków  ,
, 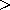 lub =.
Znak
lub =.
Znak 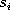 reprezentuje relację pomiędzy liczbami
reprezentuje relację pomiędzy liczbami 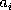 i
i 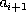 .
Na przykład, schematem monotoniczności ciągu
.
Na przykład, schematem monotoniczności ciągu 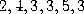 jest
jest 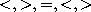 .
.
Powiemy, że ciąg liczb 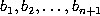 , o schemacie monotoniczności
, o schemacie monotoniczności
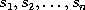 , realizuje pewien schemat monotoniczności
, realizuje pewien schemat monotoniczności
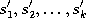 ,
jeżeli dla każdego całkowitego
,
jeżeli dla każdego całkowitego 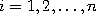 zachodzi
zachodzi 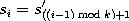 .
Innymi słowy, ciąg
.
Innymi słowy, ciąg 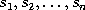 uzyskujemy, powtarzając odpowiednio
długo ciąg
uzyskujemy, powtarzając odpowiednio
długo ciąg 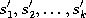 i ewentualnie odrzucając kilka ostatnich
wyrazów tego powtórzenia.
Na przykład, ciąg
i ewentualnie odrzucając kilka ostatnich
wyrazów tego powtórzenia.
Na przykład, ciąg 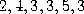 realizuje następujące schematy monotoniczności:
realizuje następujące schematy monotoniczności:
Dany jest ciąg liczb całkowitych 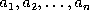 .
Twoim zadaniem jest znalezienie najdłuższego jego podciągu
.
Twoim zadaniem jest znalezienie najdłuższego jego podciągu
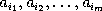 (
(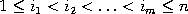 )
realizującego pewien zadany schemat monotoniczności
)
realizującego pewien zadany schemat monotoniczności 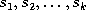 .
.
Wejście
W pierwszym wierszu standardowego wejścia znajdują się dwie liczby całkowite
 oraz
oraz 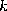 (
(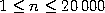 ,
, 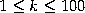 ),
oddzielone pojedynczym odstępem i oznaczające odpowiednio długość ciągu
),
oddzielone pojedynczym odstępem i oznaczające odpowiednio długość ciągu 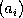 oraz długość schematu monotoniczności
oraz długość schematu monotoniczności 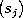 .
.
W drugim wierszu znajduje się  liczb całkowitych
liczb całkowitych 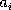 pooddzielanych
pojedynczymi odstępami, oznaczających wyrazy badanego ciągu
(
pooddzielanych
pojedynczymi odstępami, oznaczających wyrazy badanego ciągu
(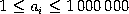 ).
).
W trzecim wierszu znajduje się 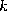 znaków
znaków 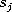 postaci <, > lub =,
pooddzielanych pojedynczymi odstępami, oznaczających kolejne wyrazy schematu monotoniczności.
postaci <, > lub =,
pooddzielanych pojedynczymi odstępami, oznaczających kolejne wyrazy schematu monotoniczności.
Wyjście
W pierwszym wierszu standardowego wyjścia Twój program powinien wypisać
jedną liczbę całkowitą 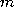 oznaczającą maksymalną długość podciągu ciągu
oznaczającą maksymalną długość podciągu ciągu
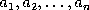 realizującego schemat monotoniczności
realizującego schemat monotoniczności 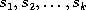 .
.
W drugim wierszu Twój program powinien wypisać dowolny przykład takiego
podciągu 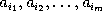 , oddzielając jego wyrazy pojedynczymi
odstępami.
, oddzielając jego wyrazy pojedynczymi
odstępami.
Przykład
Dla danych wejściowych:
7 3 2 4 3 1 3 5 3 < > =
poprawną odpowiedzią jest:
6 2 4 3 3 5 3
Autor zadania: Marian M. Kędzierski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English