
Zadanie Klocki (klo)
Pomóż nam usprawnić bazę zadań!
Klocki
Limit pamięci: 32 MB
Bajtek ma dużo klocków, którymi bardzo lubi się bawić. Niestety, ma do nich tylko jedno pudełko i to tak małe, że nie można zmieścić w nim wszystkich klocków.
Bajtek jest bardzo uporządkowanym chłopcem i nie lubi zostawiać bałaganu w swoim pokoju. Dlatego zawsze po zabawie pakuje klocki do pudełka i kładzie pudełko na półce.
Wszystkie klocki mają ten sam rozmiar, więc bez względu
na to, ile klocków wybierze, zawsze może zapakować ich do
pudełka co najwyżej 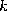 .
Chciałby jednak, aby (w miarę możliwości) na podłodze pozostały
tylko lekkie klocki, więc zawsze próbuje zapakować do pudełka
cięższe.
Czasem jednak okazuje się, że pudełko jest dla niego zbyt ciężkie,
żeby położyć je na półce - Bajtek jest przecież tylko małym chłopcem!
Stara się więc zapakować do pudełka klocki o jak największej sumarycznej
masie, tak jednak, aby był w stanie je podnieść.
.
Chciałby jednak, aby (w miarę możliwości) na podłodze pozostały
tylko lekkie klocki, więc zawsze próbuje zapakować do pudełka
cięższe.
Czasem jednak okazuje się, że pudełko jest dla niego zbyt ciężkie,
żeby położyć je na półce - Bajtek jest przecież tylko małym chłopcem!
Stara się więc zapakować do pudełka klocki o jak największej sumarycznej
masie, tak jednak, aby był w stanie je podnieść.
Bajtek ma już dość przepakowywania klocków tylko dlatego, że nie ma dość siły, aby podnieść pudełko. Poprosił więc Ciebie o napisanie programu, który powie mu, jak optymalnie upakować klocki.
Wejście
W pierwszym wierszu standardowego wejścia znajdują się trzy liczby całkowite  ,
, 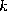 oraz
oraz  (
(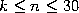 ,
, 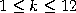 ,
, 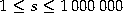 ) pooddzielane pojedynczymi
odstępami, oznaczające odpowiednio liczbę wszystkich klocków, maksymalną liczbę klocków,
które Bajtek może zmieścić w pudełku, oraz siłę Bajtka, tj. maksymalną masę pudełka,
jakie może on podnieść.
) pooddzielane pojedynczymi
odstępami, oznaczające odpowiednio liczbę wszystkich klocków, maksymalną liczbę klocków,
które Bajtek może zmieścić w pudełku, oraz siłę Bajtka, tj. maksymalną masę pudełka,
jakie może on podnieść.
W drugim wierszu wejścia znajduje się  liczb całkowitych
liczb całkowitych 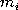 (
(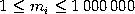 )
pooddzielanych pojedynczymi odstępami, oznaczających masy poszczególnych klocków.
)
pooddzielanych pojedynczymi odstępami, oznaczających masy poszczególnych klocków.
Masę pudełka pomijamy (możesz przyjąć, że jest równa 0).
Wyjście
W pierwszym i jedynym wierszu standardowego wyjścia Twój program powinien wypisać
jedną liczbę całkowitą 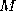 , oznaczającą maksymalną masę pudełka załadowanego klockami,
które może podnieść Bajtek.
, oznaczającą maksymalną masę pudełka załadowanego klockami,
które może podnieść Bajtek.
Przykład
Dla danych wejściowych:
3 2 5 1 3 6
poprawną odpowiedzią jest:
4
Wyjaśnienie do przykładu: Aby osiągnąć sumaryczną masę 4, Bajtek powinien włożyć do pudełka klocki o masach 1 oraz 3.
Autor zadania: Marian M. Kędzierski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English