
Zadanie Jedynki (jed)
Pomóż nam usprawnić bazę zadań!
Jedynki
Limit pamięci: 128 MB
Niech  będzie ciągiem zer i jedynek.
Skrajnie samotną jedynką (w skrócie SKS jedynką) w
będzie ciągiem zer i jedynek.
Skrajnie samotną jedynką (w skrócie SKS jedynką) w  jest skrajna (ostatnia lub pierwsza) jedynka,
która dodatkowo nie sąsiaduje bezpośrednio z żadną inną jedynką.
Na przykład, w ciągu 10001010 są dwie SKS jedynki,
w ciągu 1101011000 nie ma żadnej SKS jedynki,
a w ciągu 1000 jest tylko jedna SKS jedynka.
jest skrajna (ostatnia lub pierwsza) jedynka,
która dodatkowo nie sąsiaduje bezpośrednio z żadną inną jedynką.
Na przykład, w ciągu 10001010 są dwie SKS jedynki,
w ciągu 1101011000 nie ma żadnej SKS jedynki,
a w ciągu 1000 jest tylko jedna SKS jedynka.
Oznaczmy przez 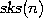 sumaryczną liczbę SKS jedynek w reprezentacjach
binarnych liczb od 1 do
sumaryczną liczbę SKS jedynek w reprezentacjach
binarnych liczb od 1 do  .
Na przykład,
.
Na przykład,
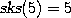 ,
, 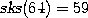 ,
, 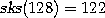 ,
, 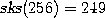 .
.
Chcemy przetwarzać bardzo duże liczby.
Będziemy je więc reprezentować w postaci zwartej.
Jeśli  jest dodatnią liczbą całkowitą,
jest dodatnią liczbą całkowitą, 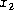 jest jej zapisem binarnym
(zaczynającym się od 1), to zwartą reprezentacją
jest jej zapisem binarnym
(zaczynającym się od 1), to zwartą reprezentacją  jest ciąg
jest ciąg 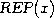 złożony z dodatnich liczb całkowitych, które odpowiadają długościom
kolejnych bloków takich samych cyfr.
Na przykład:
złożony z dodatnich liczb całkowitych, które odpowiadają długościom
kolejnych bloków takich samych cyfr.
Na przykład:
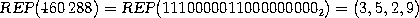
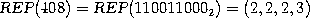
Twoim zadaniem jest napisanie programu, który oblicza ciąg 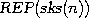 na podstawie
na podstawie 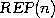 .
.
Wejście
Pierwszy wiersz standardowego wejścia zawiera jedną liczbę całkowitą 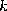 (
(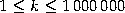 ), oznaczającą długość zwartej reprezentacji dodatniej liczby całkowitej
), oznaczającą długość zwartej reprezentacji dodatniej liczby całkowitej  .
Drugi wiersz standardowego wejścia zawiera
.
Drugi wiersz standardowego wejścia zawiera 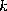 liczb całkowitych
liczb całkowitych 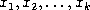 ,
(
,
( ) pooddzielanych pojedynczymi odstępami.
Ciąg liczb
) pooddzielanych pojedynczymi odstępami.
Ciąg liczb 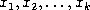 jest zwartą reprezentacją dodatniej liczby całkowitej
jest zwartą reprezentacją dodatniej liczby całkowitej  .
Dodatkowo możesz założyć, że
.
Dodatkowo możesz założyć, że 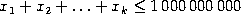 , czyli
, czyli 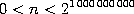 .
.
Wyjście
Twój program powinien wypisać na standardowe wyjście dwa wiersze.
W pierwszym z nich powinna znajdować się jedna dodatnia liczba całkowita 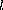 .
W drugim wierszu powinno znaleźć się
.
W drugim wierszu powinno znaleźć się 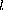 dodatnich liczb całkowitych
dodatnich liczb całkowitych 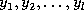 ,
pooddzielanych pojedynczymi odstępami.
Ciąg
,
pooddzielanych pojedynczymi odstępami.
Ciąg 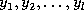 powinien być zwartą reprezentacją liczby
powinien być zwartą reprezentacją liczby 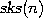 .
.
Przykład
Dla danych wejściowych:
6 1 1 1 1 1 1
poprawną odpowiedzią jest:
5 1 1 2 1 1
Wyjaśnienie do przykładu:
Ciąg 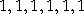 jest zwartą reprezentacją
jest zwartą reprezentacją 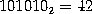 ,
, 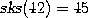 ,
natomiast
,
natomiast 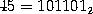 ma zwartą reprezentację
ma zwartą reprezentację 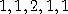 .
.
Autor zadania: Wojciech Rytter.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English