
Zadanie Monocyfrowe reprezentacje (mon)
Pomóż nam usprawnić bazę zadań!
Monocyfrowe reprezentacje
Limit pamięci: 32 MB
Niech 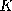 będzie cyfrą dziesiętną, różną od
będzie cyfrą dziesiętną, różną od 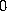 .
. 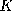 -reprezentacją liczby całkowitej
-reprezentacją liczby całkowitej 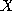 nazywamy wyrażenie arytmetyczne o wartości
nazywamy wyrażenie arytmetyczne o wartości 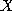 , w którym wszystkie liczby (w postaci dziesiętnej) składają się wyłącznie z cyfry
, w którym wszystkie liczby (w postaci dziesiętnej) składają się wyłącznie z cyfry 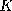 . Dopuszczalnymi działaniami w takim wyrażeniu są: dodawanie, odejmowanie, mnożenie i dzielenie. Można też używać nawiasów okrągłych. Dzielenie może wystąpić tylko wtedy, gdy dzielnik dzieli dzielną bez reszty.
. Dopuszczalnymi działaniami w takim wyrażeniu są: dodawanie, odejmowanie, mnożenie i dzielenie. Można też używać nawiasów okrągłych. Dzielenie może wystąpić tylko wtedy, gdy dzielnik dzieli dzielną bez reszty.
Przykład
Każde z poniższych wyrażeń jest 5-reprezentacją liczby 12:
- 5+5+(5:5)+(5:5)
- (5+(5))+5:5+5:5
- 55:5+5:5
- (55+5):5
Długością 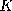 -reprezentacji nazywamy liczbę wystąpień w niej cyfry
-reprezentacji nazywamy liczbę wystąpień w niej cyfry 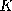 . W powyższym przykładzie dwie pierwsze reprezentacje mają długość 6, trzecia - długość 5, a czwarta - długość 4.
. W powyższym przykładzie dwie pierwsze reprezentacje mają długość 6, trzecia - długość 5, a czwarta - długość 4.
Zadanie
Napisz program, który:
- ze standardowego wejścia wczytuje cyfrę
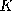 oraz ciąg liczb,
oraz ciąg liczb, - dla każdej liczby z tego ciągu sprawdza, czy istnieje jej
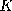 -reprezentacja nie dłuższa niż 8 i jeśli tak, to znajduje minimalną długość takiej reprezentacji,
-reprezentacja nie dłuższa niż 8 i jeśli tak, to znajduje minimalną długość takiej reprezentacji, - wypisuje wynik na standardowe wyjscie.
Wejście
Pierwszy wiersz standardowego wejścia zawiera cyfrę 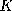 ,
, 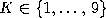 . Drugi wiersz zawiera liczbę
. Drugi wiersz zawiera liczbę  ,
, 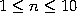 . W następnych
. W następnych  wierszach znajduje się ciąg liczb naturalnych
wierszach znajduje się ciąg liczb naturalnych  ,
, 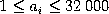 (dla
(dla 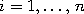 ), po jednej liczbie w każdym wierszu.
), po jednej liczbie w każdym wierszu.
Wyjście
Standardowe wyjście składa się z  wierszy. Wiersz nr
wierszy. Wiersz nr 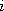 powinien zawierać:
powinien zawierać:
- dokładnie jedną liczbę będącą minimalną długością
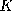 -reprezentacją
-reprezentacją 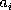 , o ile ta długość nie przekracza 8,
, o ile ta długość nie przekracza 8, - jedno słowo NIE, jeżeli minimalna długość
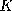 -reprezentacji liczby
-reprezentacji liczby 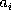 jest większa niż 8.
jest większa niż 8.
Przykład
Dla danych wejściowych:
5 2 12 31168
poprawną odpowiedzią jest:
4 NIE
Autor zadania: Krzysztof Loryś.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English