
Zadanie Sejf (B) (sej)
Pomóż nam usprawnić bazę zadań!
Safe [B]
Memory limit: 64 MB
Byteman keeps all of his savings in an old safe. The lock of this safe consists of
 identical wheels, each of them has the same word consisting of
identical wheels, each of them has the same word consisting of 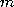 letters written on it.
Wheels can be rotated independently of each other (this way each wheel can be put in
letters written on it.
Wheels can be rotated independently of each other (this way each wheel can be put in 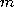 different positions).
Safe gets opened, when for all
different positions).
Safe gets opened, when for all 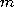 positions letters written on all wheels for that position are the same.
positions letters written on all wheels for that position are the same.
Recently one of the Byteman's acquaintance told him that it is a good idea to keep money in a bank.
Byteman decided to open his safe as soon as possible and transfer all of his money to a high-interest bank account.
Assuming that rotation of any wheel by 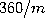 degrees to the left or to the right
can be performed within one second, calculate, how long would it take (at minimum) to open Byteman's safe.
degrees to the left or to the right
can be performed within one second, calculate, how long would it take (at minimum) to open Byteman's safe.
Task
Help Byteman!
Input
The first line of the standard input contains two integers  and
and 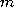 (
(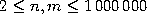 ),
separated with a single space and denoting the number of wheels in the lock and the length of the word written on each wheel.
The second line of the input contains one word
),
separated with a single space and denoting the number of wheels in the lock and the length of the word written on each wheel.
The second line of the input contains one word 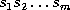 of length
of length 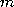 , consisting of large English letters.
In the third line there are
, consisting of large English letters.
In the third line there are  integers
integers 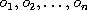 (
(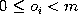 ), separated with single spaces.
), separated with single spaces.
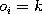 means that the word from the
means that the word from the 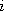 'th wheel is rotated by
'th wheel is rotated by 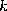 positions to the left (relatively to some defined initial position),
which means it is set in position
positions to the left (relatively to some defined initial position),
which means it is set in position 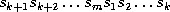 .
For instance, if
.
For instance, if 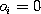 then the word on the
then the word on the 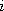 'th wheel is not rotated at all.
'th wheel is not rotated at all.
Output
The first and only line of the standard output should contain one integer, the minimal time required to open Byteman's safe.
Example
For the input data:
4 6 SLOWIK 2 0 3 5
the correct result is:
6
For the example lock, words written on each wheel look as follows:
OWIKSL
SLOWIK
WIKSLO
KSLOWI
For example, rotating the first wheel by one position to the left gives WIKSLO. When we rotate the same wheel to the right instead, we get LOWIKS.
Task author: Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English