
Zadanie Powrót klikowców (pow)
Pomóż nam usprawnić bazę zadań!
Return of the Cliquers
Memory limit: 32 MB
An undirected graph with  vertices is called a symmetric labeled cliquer if each connected
component of the graph contains the same number of vertices and is a clique, and the vertices of the graph are
numbered with numbers from the set
vertices is called a symmetric labeled cliquer if each connected
component of the graph contains the same number of vertices and is a clique, and the vertices of the graph are
numbered with numbers from the set 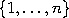 .
Maurycy has drawn all symmetric labeled cliquers on a piece of paper
and is going to assess beauty of each of them with a number from
the set
.
Maurycy has drawn all symmetric labeled cliquers on a piece of paper
and is going to assess beauty of each of them with a number from
the set 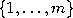 (in particular, different cliquers may be assigned equal grades).
In how many ways can he do this?
The result should be computed modulo
(in particular, different cliquers may be assigned equal grades).
In how many ways can he do this?
The result should be computed modulo  .
The figure below depicts all symmetric labeled cliquers for
.
The figure below depicts all symmetric labeled cliquers for 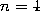 .
.
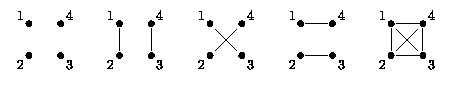
Input
The only line of the standard input contains two integers
 and
and 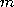 (
(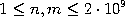 ), separated by a single space
and denoting the number of vertices of each symmetric labeled cliquer and the number of grades
respectively.
), separated by a single space
and denoting the number of vertices of each symmetric labeled cliquer and the number of grades
respectively.
Output
The only line of the standard output should contain the number of possible
sets of grades modulo  .
.
Example
For the input data:
4 2
the correct result is:
32
Task author: Tomasz Idziaszek.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English